20
LOGARITHMS
Proof of the laws of logarithms
WHEN WE ARE GIVEN the base 2, for example, and exponent 3, then we can evaluate 23.
23 = 8.
Inversely, if we are given the base 2 and its power 8 --
2? = 8
-- then what is the exponent that will produce 8?
That exponent is called a logarithm. We call the exponent 3 the logarithm of 8 with base 2. We write
3 = log28.
We write the base 2 as a subscript.
3 is the exponent to which 2 must be raised to produce 8.
A logarithm is an exponent.
Since
104 = 10,000
then
log1010,000 = 4.
"The logarithm of 10,000 with base 10 is 4."
4 is the exponent to which 10 must be raised to produce 10,000.
"104 = 10,000" is called the exponential form.
"log1010,000 = 4" is called the logarithmic form.
Here is the definition:
logbx = n means bn = x.
That base with that exponent produces x.
Example 1. Write in exponential form: log232 = 5.
Answer. 25 = 32.
| Example 2. Write in logarithmic form: 4−2 = | 1 16 |
. |
| Answer. log4 | 1 16 |
= −2. |
Problem 1. Which numbers have negative logarithms?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Proper fractions.
Example 3. Evaluate log81.
Answer. 8 to what exponent produces 1? 80 = 1.
log81 = 0.
We can observe that, in any base, the logarithm of 1 is 0.
logb1 = 0
Example 4. Evaluate log55.
Answer. 5 with what exponent will produce 5? 51 = 5. Therefore,
log55 = 1.
In any base, the logarithm of the base itself is 1.
logbb = 1
Example 5 . log22m = ?
Answer. 2 raised to what exponent will produce 2m ? Obviously, m.
log22m = m.
The following is an important formal rule, valid for any base b:
logbbx = x
This rule embodies the very meaning of a logarithm. x -- on the right -- is the exponent to which the base b must be raised to produce bx.
The rule also shows that the exponential function bx is the inverse of the function logbx. We will see this in the following Topic.
| Example 6 . Evaluate log3 | 1 9 |
. |
| Answer. | 1 9 |
is equal to 3 with what exponent? | 1 9 |
= 3−2 |
| log3 | 1 9 |
= | log33−2 = −2. |
Compare the previous rule.
Example 7. log2 .25 = ?
Answer. .25 = ¼ = 2![]() 2. Therefore,
2. Therefore,
log2 .25 = log22−2 = −2.
Example 8. log3![]() = ?
= ?
Answer. ![]() = 31/5. (Definition of a rational exponent.) Therefore,
= 31/5. (Definition of a rational exponent.) Therefore,
log3![]() = log331/5 = 1/5.
= log331/5 = 1/5.
Problem 2. Write each of the following in logarithmic form.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
| a) bn = x | logbx = n | b) 23 = 8 | log28 = 3 | |
| c) 102 = 100 | log10100 = 2 | d) 5−2 = 1/25. | log51/25 = −2. | |
Problem 3. Write each of the following in exponential form.
| a) logbx = n | bn = x | b) log232 = 5 | 25 = 32 | |
| c) 2 = log864 | 82 = 64 | d) log61/36 = −2 | 6−2 = 1/36 | |
Problem 4. Evaluate the following.
| a) log216 | = 4 | b) log416 | = 2 | |
| c) log5125 | = 3 | d) log81 | = 0 | |
| e) log88 | = 1 | f) log101 | = 0 | |
Problem 5. What number is n?
| a) log10n = 3 | 1000 | b) 5 = log2n | 32 | |
| c) log2n = 0 | 1 | d) 1 = log10n | 10 | |
| e) logn | 1 16 |
= −2 | 4 | f) logn | 1 5 |
= −1 | 5 | |
| g) log2 | 1 32 |
= n | −5 | h) log2 | 1 2 |
= n | −1 | |
Problem 6. logbbx = x
Problem 7. Evaluate the following.
| a) log9 | 1 9 |
= log99−1 = −1 |
| b) log9 | 1 81 |
= −2 | c) log2 | 1 4 |
= −2 | |||
| d) log2 | 1 8 |
= −3 | e) log2 | 1 16 |
= −4 | |||
| f) log10 .01 | = −2 | g) log10 .001 | = −3 | |
| h) log6 |
= 1/3 | i) logb |
= 3/4 | |
Common logarithms
The system of common logarithms has 10 as its base. When the base is not indicated,
log 100 = 2
then the system of common logarithms -- base 10 -- is implied.
Here are the powers of 10 and their logarithms:
| Powers of 10: | 1 1000 |
1 100 |
1 10 |
1 | 10 | 100 | 1000 | 10,000 | ||||||||
| Logarithms: | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | ||||||||
Logarithms replace a geometric series with an arithmetic series.
Problem 8. log 10n = ? n. The base is 10.
Problem 9. log 58 = 1.7634. Therefore, 101.7634 = ?
58. 1.7634 is the common logarithm of 58. When 10 is raised to that exponent, 58 is produced.
Problem 10. log (log x) = 1. What number is x?
log a = 1, implies a = 10, which is the base.
Therefore, log (log x) = 1 implies log x = 10. Since 10 is the base,
x = 1010 = 10,000,000,000
Natural logarithms
The system of natural logarithms has the number called e as its base. (e is named after the 18th century Swiss mathematician, Leonhard Euler.) e is the base used in calculus. It is called the "natural" base because of certain technical considerations.
ex has the simplest derivative. Lesson 14 of An Approach to Calculus.)
e can be calculated from the following series expressed with factorials:
| e | = 1 + | 1 1! |
+ | 1 2! |
+ | 1 3! |
+ | 1 4! |
+ . . . |
e is an irrational number; its decimal value is approximately
2.71828182845904.
To indicate the natural logarithm of a number we write "ln."
ln x means logex.
Problem 11. What number is ln e ?
ln e = 1. The logarithm of the base itself is always 1. e is the base.
Problem 12. Write in exponential form (Example 1): y = ln x.
ey = x.
e is the base.
The three laws of logarithms
1. logbxy = logbx + logby
"The logarithm of a product is equal to the sum
of the logarithms of each factor."
| 2. logb | = logbx − logby |
"The logarithm of a quotient is equal to the logarithm of the numerator
minus the logarithm of the denominator."
3. logb xn = n logbx
"The logarithm of x with a rational exponent is equal to
the exponent times the logarithm."
We will prove these laws below.
| Example 9. Apply the laws of logarithms to log | abc2 d3 |
. |
Answer. According to the first two laws,
| log | abc2 d 3 |
= | log (abc2) − log d 3 |
| = | log a + log b + log c2 − log d 3 | ||
| = | log a + log b + 2 log c − 3 log d, | ||
according to the third law.
The Answer above shows the complete theoretical steps. In practice, however, it is not necessary to write the line
| log | abc2 d 3 |
= | log (abc2) − log d 3 | . |
The student should be able to go immediately to the next line --
| log | abc2 d 3 |
= | log a + log b + log c2 − log d 3 |
-- if not to the very last line![]()
| log | abc2 d 3 |
= | log a + log b + 2 log c − 3 log d. |
| Example 10. Apply the laws of logarithms to log | z5 |
. |
| Answer. | log | z5 |
= log x + log |
Now, ![]() = y½. (Lesson 29 of Algebra.) Therefore, according to the third law:
= y½. (Lesson 29 of Algebra.) Therefore, according to the third law:
| log | z5 |
= log x + ½ log y − 5 log z. |
Example 11. Use the laws of logarithms to rewrite ln ![]() .
.
Solution.
| ln |
= | ln (sin x ln x)½ |
| = | ½ ln (sin x ln x), 3rd Law | |
| = | ½ (ln sin x + ln ln x), 1st Law. | |
Problem 13. Use the laws of logarithms to rewrite the following.
| a) log | ab c |
= log a + log b − log c | |
| b) log | ab2 c4 |
= log a + 2 log b − 4 log c | |
| c) log | z |
= 1/3 log x + 1/2 log y − log z | |
d) ln (sin2x ln x) = ln sin2x + ln ln x = 2 ln sin x + ln ln x
| e) ln |
= ½ ln (cos x· x1/3 ln x) |
| = ½ (ln cos x + 1/3 ln x + ln ln x) | |
| f) ln (a2x − 1 b5x + 1 ) | = ln a2x − 1 + ln b5x + 1 |
| = (2x − 1) ln a + (5x + 1) ln b | |
Example 12. Solve this equation for x:
| log 32x + 5 | = | 1 |
| Solution. According to the 3rd Law, we may write | ||
| (2x + 5)log 3 | = | 1. |
| Now, log 3 is simply a number. Therefore, on distributing it: | ||
| 2x· log 3 + 5 log 3 | = | 1 |
| 2x· log 3 | = | 1 − 5 log 3 |
| x | = | 1 − 5 log 3 2 log 3 |
By this technique, we can solve equations in which the unknown appears in the exponent.
Problem 14. Solve for x.
| ln 23x + 1 | = | 5. |
| (3x + 1) ln 2 | = | 5 |
| 3x ln 2 + ln 2 | = | 5 |
| 3x ln 2 | = | 5 − ln 2 |
| x | = | 5 − ln 2 3 ln 2 |
| Problem 15. Prove: −ln x | = ln | 1 x |
. |
| −ln x = (−1)ln x | = | ln | x−1, | Third law |
| = | ln | 1 x |
||
Proof of the laws of logarithms
The laws of logarithms will be valid for any base. We will prove them for base e, that is, for y = ln x.
1. ln ab = ln a + ln b.
The function y = ln x is defined for all positive real numbers x. Therefore there are real numbers p and q such that
p = ln a and q = ln b.
This implies
a = e p and b = e q.
Therefore, according to the rules of exponents,
ab = e p· e q = e p + q.
And therefore
ln ab = ln e p + q = p + q = ln a + ln b.
Which is what we wanted to prove.
In a similar manner we can prove the 2nd law. Here is the 3rd:
3. ln an = n ln a.
There is a real number p such that
p = ln a;
that is,
a = e p.
And the rules of exponents are valid for all rational numbers n (Lesson 29 of Algebra; an irrational number is the limit of a sequence of rational numbers). Therefore,
an = e pn.
This implies
ln an = ln e pn = pn = np = n ln a.
That is what we wanted to prove.
Change of base
Say that we know the values of logarithms of base 10, but not, for example, in base 2. Then we can convert a logarithm in base 10 to one in base 2 -- or any other base -- by realizing that the values will be proportional.
Each value in base 2 will differ from the value in base 10 by the same constant k.
Now, to find that constant, we know that
![]()
Therefore, on putting x = 2 above:
![]()
That implies
![]()
Therefore,
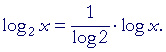
That is,
![]()
By knowing the values of logarithms in base 10, we can in this way calculate their values in base 2.
In general, then, if we know the values in base a, then the constant of proportionality in changing to base b, is the reciprocal of its log in base a.
![]()
Problem 16. Write the rule for changing to base 8 from base e.
![]()
Next Topic: Logarithmic and exponential functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
