7
THE ROOTS, OR ZEROS,
OF A POLYNOMIAL
The roots, or zeros, of a polynomial
IN THIS TOPIC we will present the basics of drawing a graph.
1. What is a polynomial equation?
It is a polynomial set equal to 0. P(x) = 0.
P(x) = 5x3 − 4x2 + 7x − 8 = 0
2. What do we mean by a root, or zero, of a polynomial?
It is a solution to the polynomial equation, P(x) = 0.
It is that value of x that makes the polynomial equal to 0.
In other words, the number r is a root of a polynomial P(x)
if and only if P(r) = 0.
Example 1. Let P(x) = 5x3 − 4x2 + 7x − 8. Then a root of that polynomial is 1 because, according to the definition:
| P(1) | = | 5· 13 − 4· 12 + 7· 1 − 8 |
| = | 5 − 4 + 7 − 8 | |
| = | 0. | |
It is traditional to speak of a root of a polynomial. Of a function in general, we speak of a zero.
Example 2. The roots of this quadratic
x2 −x − 6 = (x + 2)(x − 3)
are −2 and 3. Those are the values of x that will make the polynomial equal to 0.
3. What are the x-intercept and y-intercept of a graph?
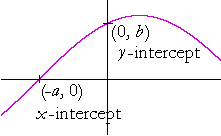
The x-intercept is that value of x where the graph crosses or touches the x-axis. At the x-intercept -- on the x-axis -- y = 0.
The y-intercept is that value of y where the graph crosses the y-axis. At the y-intercept, x = 0.
4. What is the relationship between the root of a polynomial
4. and the x-intercepts of its graph?
The roots are the x-intercepts!
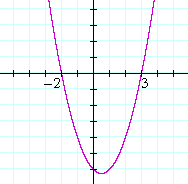
The roots of x2 −x − 6 are −2 and 3. Therefore, the graph of
y = x2 −x − 6
will have the value 0 -- it will cross the x-axis -- at −2 and 3.
5. How do we find the x-intercepts of the graph of any function
5. y = f(x)?
Solve the equation, f(x) = 0.
Problem 1.
a) Find the root of the polynomial 2x + 10.
We must solve the equation,
2x + 10 = 0. The solution is x = −5.
b) Where is the x-intercept of the graph of y = 2x + 10?
At x = −5. The x-intercept is the root.
Problem 2.
a) If a product of factors is 0 -- if ab = 0 -- then what may we conclude
a) about the factors a, b ?
Either a = 0, or b = 0.
b) Name the roots of this polynomial:
f(x) = (x + 4)(x + 2)(x − 1)
−4, −2, 1.
c) Sketch the graph of f(x). That is, sketch a continuous curve and
c) show its x-intercepts.
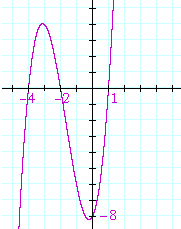
The x-intercepts are the roots.
As for the y-intercept, it is the value of y when x = 0. Therefore, the y-intercept of a polynomial is simply the constant term, which is the product of the constant terms of all the factors. (See Topic 6, Example 9.)
As for finding the turning points, that hill and valley, that will have to wait for calculus.
For roots of polynomials of degree greater than 2, see Topic 13.
Next Topic: The slope of a straight line
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
