TheMathPage

The Evolution of the

R E A L  N U M B E R S

6

UNIT FRACTIONS

A UNIT -- One -- is the source of a number of anything. We count units.

A unit fraction is a fraction whose numerator is 1.

1
2		  ,   1
3		  ,   1
4		  ,   1
5		  ,  etc.
Here is how we count  1
5		 's:

"One fifth, two fifths,three fifths,"

and so on.

Every fraction is thus a number of unit fractions.

A sum of unit fractions

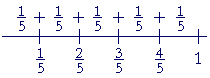
In the fraction  3
5		 , the unit is  1
5		 .  And there are 3 of them.
3
5		  =  1
5		  +  1
5		  +  1
5		 .

The denominator of a fraction names the unit  The numerator tells their number -- how many.

  Example.   In the fraction  5
6		  , what number is the unit, and

how many of them are there?

  Answer.   The unit is  1
6		 .  And there are 5 of them.
5
6		  = 5 ×  1
6		  =  1
6		  +  1
6		  +  1
6		  +  1
6		  +  1
6		 .

Problem 1.   Which numbers are the decimal unit fractions?

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").

.1, .01, .001, .0001, etc.

  Problem 2.   Let   1
3		   be the unit, and count to 2 1
3		 .
" 1
3		  ,   2
3		  ,   3
3		   or 1.  1 1
3		  ,  1 2
3		  ,  2.  2 1
3		  . "

Again:  Each fraction is a number of unit fractions.

3
5		   =  3 ×  1
5		   =   1
5		  +  1
5		  +  1
5		 .

Problem 3.

   a)    4
9		   =    4 ×  1
9		     b)    5
8		   =  5 ×  1
8
   c)   2 3
5		   =  13 ×  1
5		      d)   .35  =  35 ×  .01

Problem 4.   Write each of the following as a sum of unit fractions.

   a)    2
3		   =   1
3		  +  1
3		      b)    3
8		   =   1
8		  +  1
8		  +  1
8
   c)   1 1
4		   =   5
4		  =  1
4		  +  1
4		  +  1
4		  +  1
4		  +  1
4

Problem 5.

   a)   What number is the largest unit fraction?   1
2

b)   What number is the smallest?   There is none.

Problem 6.   1 is equal to

   a)    3
3		   b)    4
4		   c)    5
5		   d)    10
10		   e)    16
16		   f)    100
100
   g)   5 ×  1
5		      h)   9 ×  1
9		      i)   24 ×   1 
24

We see:

1 is a multiple of every unit fraction.
We can write 1 with any denominator.

   Problem 7.   What is the first multiple of    1 
32		   that will be

greater than 1?

 33
 32

For more on unit fractions, see Lesson 21 of Arithmetic.


End of Section

Next Topic:  Rational Numbers


Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com