Lesson 16 Section 2
HOW TO TAKE HALF
OF ANY NUMBER
| 7. | Which natural numbers are called the even numbers? |
| Numbers that can be divided into two equal parts. | |
8 is an even number because we can divide it "evenly" into two 4's.
![]()
4 is half of 8.
9 is not an even number. There is an "odd" 1:
![]()
Therefore we call 9 an odd number. We cannot take half of a natural number that is odd. We cannot take half of 9 people.
The even numbers, then, are the numbers divisible by 2: 2, 4, 6, 8, and so on. The odd numbers are 1, 3, 5, 7, and so on.
If you do not know half of some even number, you can find it by decomposing it mentally into two even numbers whose half you do know. We saw how to do that in Section 1, Example 8.
Example 1. How much is half of 54?
| Answer. Half of 54 | = | Half of 50 + Half of 4 |
| = | 25 + 2 | |
| = | 27. | |
As for odd numbers, note that every odd number is equal to an even number plus 1.
3 = 2 + 1.
5 = 4 + 1.
7 = 6 + 1.
9 = 8 + 1.
And so on.
Again, if a natural number is odd, then we cannot take half of it. Therefore, we will now assume that we are not necessarily dealing with natural numbers, and that 1 is now a continuous unit -- a unit we use to measure -- and that has a half: 1 minute, 1 centimeter, 1 pound, and so on. (Lesson 20.)
| 8. | What number is half of 1? |
| ½ ("One-half") | |
½ must be one half of something. It is one half of 1.
Half of $1, of course, is $.50.
| 9. | How can we take half of an odd number? |
| Half of 7 | |
| Take half of its even part, and add half of 1. | |
Example 2. How much is half of 7?
Answer. 7 = 6 + 1. Half of 6 is 3; half of 1 is ½; therefore half of 7
is 3½.
Half of $7.00 is $3.50.
Example 3. A scarf that normally sells for $17 is being sold at half price. What do you pay?
Answer. 17 = 16 + 1. Half of 16 is 8. Therefore, half of $17 is $8.50.
Example 4. How much is half of 25%?
Answer. 12½%.
25 = 24 + 1. Half of 24 is 12. Half of 1 is ½.
And so if you knew that 25% means a quarter, then you now know that 12½% means an eighth.
(See Lesson 27, Example 7.)
Example 5 How much is half of $27.40?
Answer. We will take half of $27 and add it to half of $.40.
Since 27 = 26 + 1, then
Half of $27 is $13.50.
Half of $.40 is $.20.
Therefore, half of $27.40 is $13.70.
Example 6. How much is half of 90?
Answer. 90 = 80 + 10. Half of 80 is 40; half of 10 is 5; therefore half of 90 is 45.
See Problem 21.
Example 7. How much is half of $9.70?
Answer. Half of $9.00 (8 + 1) is $4.50. Half of $.70 is $.35. Therefore half of $9.70 is $4.85.
Example 8. The famous number π ("pi") is approximately 3.14. How
| much is half of π; that is, | π 2 |
? |
Answer. Ignore the decimal point in 3.14. Then half of 300 is 150; half of 14 is 7; therefore half of 314 is 157. On replacing the decimal point,
| π 2 |
| 10. | How can we take a fourth or 25% of a number? |
| Take half of half. | |
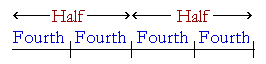
To divide a number in Half means to divide it into two equal parts. To divide it into Fourths, or quarters, means to divide it into four equal parts. And we can do that by taking half of each Half.
A quarter is half of a half. Compare Lesson 15.
Example 9. How much is a fourth, or a quarter, of 60?
Answer. Half of 60 is 30. Half of 30 is 15.
Example 10. How much is 25% of 180?
Answer. 25% means a fourth. (Lesson 15.) Half of 180 is 90. Half of 90 is 45.
Example 11. How much is 25% of 112?
Answer. Half of 112 = Half of 100 + Half of 12 = 56.
Answer. Half of 56 = Half of 50 + Half of 6 = 25 + 3 = 28.
Example 12. How much is 25% of $9.60?
Answer. Half of $9.60 = $4.50 + $.30 = $4.80. Half of $4.80 = $2.40
| 11. | How can we multiply by 5? |
| 5 × 123 | |
| Take half of the multiplication by 10. | |
Since 5 is half of 10, then 5 times a number will be half of 10 times that number.
Example 13. 5 × 123 = Half of 10 × 123
Example 13 5 × 123 = Half of 1230 (Lesson 4, Question 1.)
Example 13. 5 × 123 = 615.
Example 14. 5 × $1.50 = Half of $15
Example 14. 5 × $1.50 = $7.50.
Example 15. 5 × $46.80 = Half of $468
Example 15. 5 × $46.80 = $234.
| 12. | How can we take 5% of a number? |
| Take half of 10%. | |
Example 16. How much is 5% of $162?
Answer. 10% is $16.20. (Lesson 4, Question 7.) Therefore, 5% is $8.10.
To write .05 and multiply, is a written method for those who do not understand percent.
Example 17. How much is 5% of $475?
Answer. 10% is $47.50. Therefore, 5% is $23.50 + $.25 = $23.75.
| 13. | How can we multiply by 15? |
| 15 × 8 | |
| Multiply by 10, and add half. | |
For, 15 = 10 + Half of 10.
Example 18. 15 × 8 = 80 + Half of 80
Example 18. 15 × 8 = 80 + 40
Example 18. 15 × 8 = 120.
Example 19. 15 × 42 = 420 + 210.
Example 19. 15 × 42 = 630.
| 14. | How can we take 15% of a number? |
| Take 10% and add half. | |
Example 20. How much is 15% of $70??
| Answer. 15% | = | 10% + Half of 10% |
| = | $7.00 + $3.50 | |
| = | $10.50. | |
Example 21. If you tip at the rate of 15%, and the bill is $40, how much do you leave?
| Answer. 15% | = | 10% + Half of 10% |
| = | $4.00 + $2.00 | |
| = | $6.00. | |
At this point, please "turn" the page and do some Problems.
or
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
