Lesson 21
UNIT FRACTIONS
In this Lesson, we will answer the following:
A unit -- "one" -- is the source of a number of anything.
We count units.
| 1. | What is a unit fraction? |
| A fraction with 1 as its numerator. | |
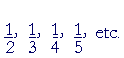
Each unit fraction is a part of number 1. Half of 1, a third, a fourth, and so on.
Here is how we count ![]() 's. "One fifth, two fifths, three fifths," and so on.
's. "One fifth, two fifths, three fifths," and so on.
Every fraction is thus a number of unit fractions.
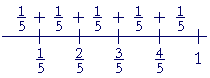
| In the fraction | 3 5 |
, the unit is | 1 5 |
. And there are 3 of them. |
| 3 5 |
= | 1 5 |
+ | 1 5 |
+ | 1 5 |
. |
The denominator of a fraction names the unit The numerator tells their number -- how many.
Example 1. In the fraction ![]() , what number is the unit, and how many of them are there?
, what number is the unit, and how many of them are there?
| Answer. The unit is | 1 6 |
. And there are 5 of them. |
| 5 6 |
= 5 × | 1 6 |
= | 1 6 |
+ | 1 6 |
+ | 1 6 |
+ | 1 6 |
+ | 1 6 |
. |
| Example 2. Let | 1 3 |
be the unit -- and count to 2 | 1 3 |
. |
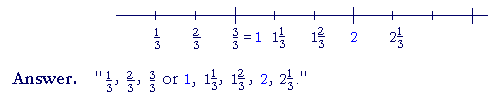
Again, every fraction is a sum -- a number -- of unit fractions.
| 2 3 |
= 2 × | 1 3 |
= | 1 3 |
+ | 1 3 |
. |
| 3 8 |
= 3 × | 1 8 |
= | 1 8 |
+ | 1 8 |
+ | 1 8 |
. |
The symbols for all the numbers of arithmetic
stand for a sum of units.
| Example 3. Add | 2 8 |
+ | 3 8 |
. |
| Answer. | 5 8 |
. |
2 eighths + 3 eighths are 5 eighths. The unit we are adding is ![]() .
.
This illustrates the following principle:
We can only add or subtract things that have the same name,
which we call the unit.
In the Example above , the name of what we are adding is "Eighths."
We will see this in Lesson 25. The denominator of a fraction has no other function but to name the unit.
| 5 9 |
− | 3 9 |
= | 2 9 |
. |
Example 4. 1 is how many fifths?
| Answer. 1 = | 5 5 |
("Five fifths.") | ||||||||
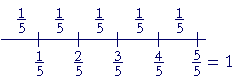
| 1 5 |
is contained in 1 five times. |
Similarly,
| 1 = | 3 3 |
= | 4 4 |
= | 10 10 |
And so on. We may express 1 as a fraction with any denominator.
Example 5. Add, and express the sum as an improper fraction:
| 5 9 |
+ 1. |
| Answer. | 5 9 |
+ 1 = | 5 9 |
+ | 9 9 |
= | 14 9 |
. |
It was necessary to express 1 as so many ninths because whatever we add must have the same name.

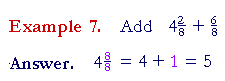
| 2. | How can we express a whole number as fraction with a given denominator? |
| Multiply the denominator by the whole number. Make that product the numerator. | |
| Example 8. 2 = | 2 × 5 5 |
= | 10 5 |
. |
| Since 1 = | 5 5 |
, then 2 is twice as many fifths: |
| 2 = | 10 5 |
. 3 = | 15 5 |
. 4 = | 20 5 |
. |
And so on.
| Example 9. 6 = | ? 3 |
| Answer. 6 = | 6 × 3 3 |
= | 18 3 |
. |
| Example 10. How many times is | 1 8 |
contained in 5? |
| That is, 5 = | ? 8 |
. |
| Answer. 5 = | 40 8 |
. |
| Example 11. Add: | 5 3 |
+ 4. |
| Answer. | 5 3 |
+ 4 = | 5 3 |
+ | 12 3 |
= | 17 3 |
= 5 | 2 3 |
. |
Let us now revisit the rule for changing a mixed number to an improper fraction (Lesson 20). In fact, we will see why we have that rule.
| 3. | How do we change a mixed number to an improper fraction? |
| Change the whole number to a fraction with the same denominator. Then add those fractions. | |
| Example 12. 3 | 5 8 |
= 3 + | 5 8 |
= | 24 8 |
+ | 5 8 |
= | 29 8 |
. |
| Example 13. 5 | 2 7 |
= 5 + | 2 7 |
= | 35 7 |
+ | 2 7 |
= | 37 7 |
. |
The complement of a proper fraction
| 4. | What do we mean by the complement of a proper fraction? |
|
|
|
| It is the proper fraction we must add in order to get 1. | |
Example 14.
![]() + ? = 1.
+ ? = 1.
Answer. Since 1 = ![]() , then
, then ![]() +
+ ![]() = 1.
= 1.
![]() is called the complement of
is called the complement of ![]() .
. ![]() completes
completes ![]() to make 1.
to make 1.
Equivalently, since finding what number to add is subtraction:
| 1 − | 5 8 |
= | 3 8 |
. |
| Example 15. 1 − | 3 5 |
= | 2 5 |
. |
| When we add | 2 5 |
to | 3 5 |
, we get | 5 5 |
, which is 1. |
| 2 5 |
is the complement of | 3 5 |
. |
Example 16. Compare
| 1 − | 1 4 |
and 6 − | 1 4 |
. |
| First, since 1 is | 4 4 |
, then |
| 1 − | 1 4 |
= | 3 4 |
, |
| which is the complement of | 1 4 |
. |
Look:
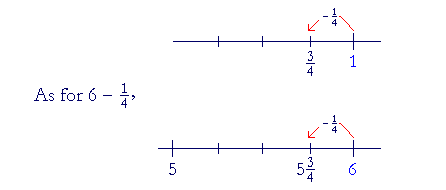
since we are subtracting ![]() -- which is less than 1 -- from 6, the
answer will fall beween 5 and 6. It will be 5
-- which is less than 1 -- from 6, the
answer will fall beween 5 and 6. It will be 5![]() .
.
Again, ![]() is the complement of
is the complement of ![]() .
.
| 5. | What will be the answer when we subtract a proper fraction from a whole number greater than 1? |
|
|
|
| It will be the mixed number that is one whole number less, and whose fraction is the complement of the proper fraction. | |
| Example 17. | 5 − | 1 3 |
= 4 | 2 3 |
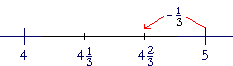
| 4 is one less than 5. And | 2 3 |
is the complement of | 1 3 |
. |
In fact, whenever we subtract ![]() from a whole number, the fractional part will be
from a whole number, the fractional part will be ![]() .
.
| 12 − | 1 3 |
= | 11 | 2 3 |
. |
| 25 − | 1 3 |
= | 24 | 2 3 |
. |
| 38 − | 1 3 |
= | 37 | 2 3 |
. |
And so on.
| Example 18. 9 − | 2 5 |
= 8 | 3 5 |
. |
We could even check that by adding:
| 8 | 3 5 |
+ | 2 5 |
= 8 | 5 5 |
= 9. |
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
