S k i l l
i n
A R I T H M E T I C

Lesson 21

EQUIVALENT FRACTIONS

In this Lesson, we will answer the following:

What are equivalent fractions?
How do we convert a fraction to an equivalent fraction with a larger denominator?
When the denominators of two fractions have no common divisors, and we want to convert them to equivalent fractions with equal denominators,
what denominator should we choose?
How do we reduce a fraction to its lowest terms?
Section 2
How can we reduce a fraction in which the numerator or denominator is a decimal?

1.	What are equivalent fractions?

	Equivalent fractions are fractions with different names but equal value. They are at the same place on the number line.

Here is an elementary example:

1
2

2
4

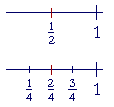
1
2

is 1 of 2 equal parts of 1.

2
4

is 2 of 4 equal parts. Each fraction is

one half of 1.

Relative to a unit of measure, equivalent fractions are equal measurements.

1
2

inch =

2
4

inch.

2.	How do we convert a fraction to an equivalent fraction with a larger denominator?

	Multiply the original denominator so that it equals the larger denominator. Multiply the numerator by the same number.

2
3

2 × 5
3 × 5

10
15

This follows from Lesson 19, Questions 13, 14 and 15.

Example 1. Write the missing numerator:

6
7

?
28

Answer. To make 28, we have to multiply 7 by 4. Therefore, we must also multiply 6 by 4:

6
7

4 × 6
28

4 × 7

In practice, to find the multiplier, divide the original denominator into the new denominator, and then multiply the numerator by that quotient. That is, say:

"7 goes into 28 four times. Four times 6 is 24."

The student who has studied ratio and proportion, will recognize this as the theorem of the same multiple (Lesson 17, Question 3). In fact, everything we know about ratios carries over into fractions; for, numerators and denominators being natural numbers, each numerator has a ratio to its denominator.

Example 2. Write the missing numerator:

5
8

?
48

Answer. "8 goes into 48 six times. Six times 5 is 30."

5
8

30
48

Example 3. Name three fractions that are equivalent to

3
4

Answer. For example,

6
8

9
12

21
28

To create them, we multiplied both 3 and 4 by the same number. First by 2, then by 3, then by 7.

In actual problems, we convert two (or more) fractions so that they have equal denominators. When we do that, it is easy to compare them (see the next Lesson, Question 3), and it is necessary in order to add or subtract them (Lesson 24); for we can only add or subtract quantities that have the same name, that is, that are units of the same kind; and it is the denominator of a fraction that names the unit. (Lesson 20.)

In fact:

When the denominators of two fractions have no common divisors, and we want to convert them to equivalent fractions with equal denominators,
what denominator should we choose?

2
3

and

4
5

Choose the product of the denominators.

Example 4. Convert

2
3

and

4
5

to equivalent fractions with equal

denominators.

Answer. The denominators 3 and 5 have no common divisors (except 1). Therefore, as a common denominator, choose 15.

2
3

10
15

4
5

12
15

To convert

2
3

, we said, "3 goes into 15 five times. Five times 2 is 10."

To convert

4
5

, we said, "5 goes into 15 three times. Three times 4 is 12."

Once we convert to a common denominator, we could then know

that

4
5

is greater than

2
3

. Because when fractions have equal

denominators, then the larger the numerator, the larger the fraction. (Lesson 19, Question 12.)

Also, we could now add those fractions:

2
3

4
5

10
15

12
15

22
15

See Lesson 20, Example 3.

We can choose the product of denominators even when the denominators have a common divisor. But their product will not then be their lowest common multiple (Lesson 22). The student should prefer the lowest common multiple, because smaller numbers make for simpler calculations.

Same ratio

When fractions are equivalent, their numerators and denominators are in the same ratio. (That in fact is the best definition of equivalent fractions, because it tells us how to know when fractions are equivalent)

1
2

2
4

1 is half of 2. 2 is half of 4. In fact, any fraction where the numerator

is half of the denominator will be equivalent to

1
2

2
4

3
6

5
10

8
16

1 is half of 2. 2 is half of 4. 3 is half of 6. 5 is half of 10. And so on. These are all at the same place on the number line.

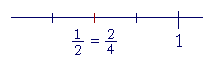
Example 5.

4
12

and

5
15

are equivalent, because each numerator is a third

of its denominator.

Example 6. Write the missing numerator:

7
28

?
16

Answer. 7 is a quarter of 28. And a quarter of 16 is 4.

7
28

4
16

7 is to 28 as 4 is to 16.

7
28

and

4
16

are equivalent.

How to simplify or reduce a fraction

The numerator and denominator of a fraction are called its terms. To simplify or reduce a fraction means to make the terms smaller. To accomplish that, we divide both terms by a common divisor. (Again, see Lesson 19.)

Example 7.

24
36

24 ÷ 4
36 ÷ 4

6
9

6 ÷ 3
9 ÷ 3

2
3

24
36

6
9

, and

2
3

are equivalent fractions. Of those three

equivalents,

2
3

has the lowest terms -- we cannot divide any further. We

like to express a fraction with its lowest terms, because it gives a better sense of its value, and it makes for simpler calculations.

4.	How do we reduce a fraction to its lowest terms?

	Keep dividing both terms by a common divisor.

Example 8. Reduce to lowest terms:

20
24

Answer. 20 and 24 have a common divisor, 4.

20
24

"4 goes into 20 five times."
6

"4 goes into 24 six times."

(See also Lesson 16, Question 7.)

Example 9. Reduce

500
1500

Answer. When the terms have the same number of 0's, we may ignore them.

500
1500

5
15

1
3

Effectively, we have divided 500 and 1500 by 100. (Lesson 1, Question 11.)

Example 10. Write as a mixed number:

20
8

Solution. Divide 20 by 8. "8 goes into 20 two (2) times (16) with 4 left over."

20
8

= 2

4
8

= 2

1
2

4
8

is equivalent to

1
2

Or, we could reduce first. 20 and 8 have a common divisor 4:

20 8	=	5 "4 goes into 20 five times." 2 "4 goes into 8 two times."

	=	2½.

Notice that we are free to interpret the same symbol

20
8

in various ways. It is the fraction

20
8

. It is 20 divided by 8. And it signifies

"the ratio of 20 to 8."

Example 11. Reduce

5
5

Answer.

5
5

= 1.

Any fraction in which the numerator and denominator are equal, is equal to 1.

Summary

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: themathpage@nyc.rr.com