The equation and graph of a straight line: Section 2
Drawing the graph
The x- and y-intercepts of a graph
The x- and y-intercepts of a graph
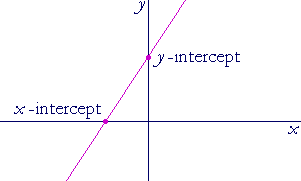
The x-intercept of a graph is that value of x where the graph crosses the x-axis. The y-intercept is the value of y where it crosses the y-axis.
To find the x-intercept, we have to find the value of x where y = 0 -- because at every point on the x-axis, y = 0.
Example 1. Calculate the value of x when y = 0, that is, find the x-intercept of y = 2x + 10.
Solution. On putting y = 0, we have to solve the equation,
| 2x + 10 | = | 0. | |
| We have: | |||
| 2x | = | −10 | |
| x | = | −5. | |
The x-intercept is −5.
Problem 10. Calculate the value of x when y = 0.
| a) | y | = | 2x + 4 | b) | y | = | 3x − 12 | |
| 2x + 4 | = | 0 | 3x − 12 | = | 0 | |||
| 2x | = | −4 | 3x | = | 12 | |||
| x | = | −2 | x | = | 4 | |||
| c) | y | = | 4x + 1 |
| 4x + 1 | = | 0 | |
| 4x | = | −1 | |
| x | = | −¼ | |
To find the y-intercept of a graph, we must find the value of y when x = 0 -- because at every point on the y-axis, x = 0. But when the equation has the form
y = ax + b,
the y-intercept is simply b. When x = 0,
y = 0 + b = b.
Drawing the graph
Two points determine a straight line. And the two most important points are the x- and y-intercepts. Therefore whenever we draw a graph, we always mark those points.
Problem 11.
| a) | When we have the equation of a straight line, how do we find the x−intercept? |
Put y =0 and solve for x.
b) How do we find the y−intercept?
Put x =0 and solve for y.
Problem 12. Mark the x- and y-intercepts, and draw the graph of
y = 2x + 6.
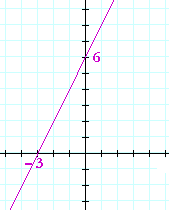
The x-intercept −3 is the solution to 2x + 6 = 0. The y-intercept is the constant term, 6. The graph is the straight line that passes through those two intercepts.
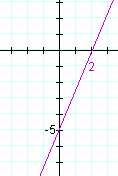
Example 2. Mark the x- and y-intercepts, and draw the graph of
5x − 2y = 10.
Solution. Although this does not have the form y = ax + b, the strategy is the same. Find the intercepts by putting x -- then y -- equal to 0.
| x | y | ||
| y-intercept | 0 | −5 | |
| 2 | 0 | x-intercept |
When we put x = 0, we have
| −2y | = | 10. | |
| This implies | |||
| y | = | −5. | |
When we put y = 0, we have
| 5x | = | 10. | |
| This implies | |||
| x | = | 2. | |
Here is the graph:
Problem 13.
| a) | In an equation y = ax + b , where on the graph do we find b? |
As the y-intercept.
| b) | Where do we find the solution to ax + b = 0 ? |
As the x-intercept.
Problem 14. Mark the x− and y−intercepts, and draw the graph.
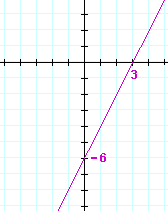
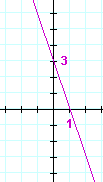
| a) | y = 2x − 6 | b) | y = −3x + 3 | |
 |
 |
|||
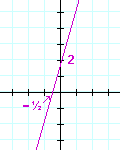
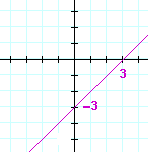
| c) | y = 4x + 2 | d) | x − y = 3 | |
 |
 |
|||
| See Example 2. | ||||
| e) | x − 2y + 2 = 0 | f) | 2x − 3y − 6 = 0 | |
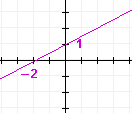 |
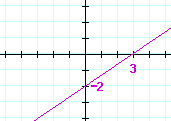 |
|||
| g) | y = −x + 1 | h) | y = 6x − 3 | |
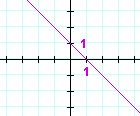 |
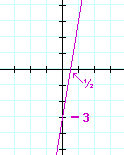 |
|||
Problem 15. The form y = ax.
| a) | When an equation has the form y = ax (for example, y = 2x), what number is b ? 0 |
| b) | Therefore, what number is the y-intercept? 0 |
c) Through which point does the line pass?
The origin. In other words the x- and y- intercepts coincide.
d) How do we find another point on the line?
Choose any value for x. The equation will then determine the value of y.
(In the next Lesson, we will see that a is the slope of the line.
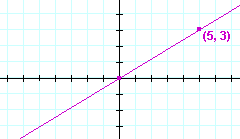
Example 3. Draw the graph of y = 2x.
Solution. Since b = 0, the graph passes through the origin. To find another point, let x = 1 for example. Then y = 2 · 1 = 2. The point (1, 2) is on the graph:
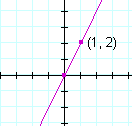
| Example 4. Draw the graph of y = | 2 3 |
x. |
Solution. Again, since b = 0, the graph passes through the origin. To find another point, choose an integer value for x in such a way that y also will be an integer. Choose x equal to the denominator, 3. The point (3, 2) then is on the graph.
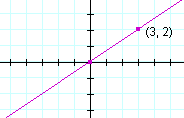
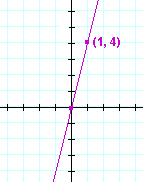
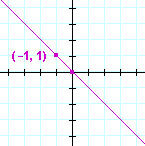
Problem 16. Draw each graph.
| a) | y = 4x | b) | y = −x | |
 |
 |
|||
| c) | y = | 3 5 |
x | d) | y = − | 2 5 |
x |
 |
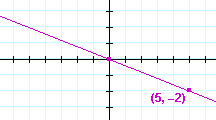 |
Example 6. Vertical and horizontal lines.
An equation of the form
x = A number
is the equation of a vertical line. For example,
x = 3.
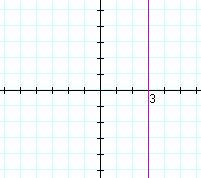
x = 3 -- the x-coördinate is 3 -- is true of every point on that line.
An equation of the form
y = A number
is the equation of a horizontal line. For example,
y = −4.
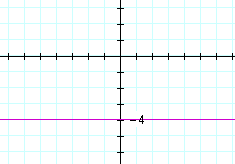
The y-coördinate is −4 at every point on that line.
Problem 17. Draw each graph.
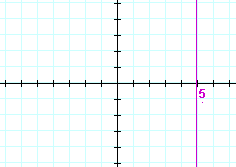
| a) | x = 5 | b) | x = −2 | |
 |
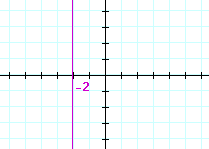 |
|||
| c) | y = 3 | d) | y = −1 | |
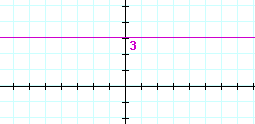 |
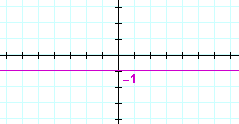 |
|||
Problem 18.
a) What is the equation of the x-axis?
y = 0
b) What is the equation of the y-axis?
x = 0
Next Lesson: The slope of a straight line
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com