21
NEGATIVE EXPONENTS
Power of a fraction
"To raise a fraction to a power, raise the numerator
and denominator to that power."
| Example 1. |  |
For, according to the meaning of the exponent, and the rule for multiplying fractions:
| Example 2. Apply the rules of exponents: |  |
Solution. We must take the 4th power of everything. But to take a power of a power -- multiply the exponents:
Problem 1. Apply the rules of exponents.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) |  |
= | x² y² |
b) |  |
= | 8x³ 27 |
c) |  |
= | 
|
| d) |  |
= | 
|
| e) |  |
= | x² − 2x + 1 x² + 2x + 1 |
Perfect Square Trinomial |
Subtracting exponents
In the previous Lesson we saw the following rule for canceling:
| ax ay |
= | x y |
"If the numerator and denominator have a common factor,
it may be canceled."
Consider these examples of canceling:
| 2· 2· 2· 2· 2 2· 2 |
= | 2· 2· 2 |
| ___2· 2___ 2· 2· 2· 2· 2 |
= | __1__ 2· 2· 2 |
If we write these examples with exponents, then
 22 |
= | 23 |
| 2² 25 |
= | 1 23 |
In each case, we subtract the exponents. But when the exponent in the denominator is larger, we write 1-over their difference.
| Example 3. |  x3 |
= | x5 |
 x8 |
= | 1 x5 |
|
Here is the rule:
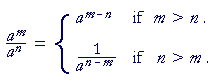
Problem 2. Simplify the following. (Do not write a negative exponent.)
| a) |  |
= | x3 | b) | x² x5 |
= | 1 x3 |
c) | x x5 |
= | 1 x4 |
| d) | x² x |
= | x | e) |  |
= | −x4 | f) |  |
= | 1 x² |
Problem 3. Simplify each of the following. Then calculate each number.
| a) |  |
= | 23 | = | 8 | b) | 2² 25 |
= | 1 23 |
= | 1 8 |
c) | 2 25 |
= | 1 24 |
= | 1 16 |
| d) | 2² 2 |
= | 2 | e) |  |
= | −24 | = | −16 | f) |  |
= | 1 2² |
= | 1 4 |
| Example 4. Simplify by reducing to lowest terms: |  |
Solution. Consider each element in turn:
Problem 4. Simplify by reducing to lowest terms. (Do not write negative exponents.
| a) |  |
= | y³ 5x³ |
b) |  |
= | − | 8a³ 5b³ |
| c) |  |
= | − | 3z_ 5x4y3 |
d) |  |
= | c³ 16 |
| e) | (x + 1)³ (x − 1) (x − 1)³ (x + 1) |
= | (x + 1)² (x − 1)² |
Negative exponents
We are now going to extend the meaning of an exponent to more than just a positive whole number. We will do that in such a way that the usual rules of exponents will hold. That is, we will want the following rules to hold for any exponents: positive, negative, 0 -- even fractions
| aman | = | am + n | Same Base |
| (ab)n | = | anbn | Power of a Product |
| (am)n | = | amn | Power of a Power |
We begin by defining a number with a negative exponent to be the reciprocal of that power with a positive exponent.
| a−n | = | 1 an |
a−n is the reciprocal of an.
| Example 5. | 2−3 | = | 1 23 |
= | 1 8 |
The base, 2, does not change. The negative exponent becomes positive -- in the denominator.
Example 6. Compare the following. That is, evaluate each one:
3−2 −3−2 (−3)−2 (−3)−3
| Answers. | 3−2 | = | 1 32 |
= | 1 9 |
Next,
−3−2 is the negative of 3−2. The base is still 3.
| −3−2 | = − | 1 9 |
As for (−3)−2, the parentheses indicate that the base is −3:
| (−3)−2 | = | 1 (−3)2 |
= | 1 9 |
Finally,
| (−3)−3 | = | 1 (−3)3 |
= | − | 1 27 |
A negative exponent, then, does not produce a negative number. Only a negative base can do that. And the exponent must be odd
| Example 7. Simplify | a² a5 |
. |
Solution. Since we have invented negative exponents, we can now subtract any exponents as follows:
| a² a5 |
= a2 − 5 = a−3 |
That is, we now have the following rule for any exponents m, n:
| In fact, we defined a− n as | 1 an |
because we want that rule |
to hold. We want
 |
= | a−3 |
But
|
= | 1 a3 |
| Therefore, we define a−3 as | 1 a3 |
. |
| Example 8. | a−1 | = | 1 a |
a−1 is now a symbol for the reciprocal, or multiplicative inverse, of any number a. It appears in the following rule (Lesson 5):
a· a−1 = 1
Problem 5.
| a) | (log 2)(log 2)−1 = 1 | b) | (x² − 7x + 5)· (x² − 7x + 5)−1 = 1 |
| c) ( | 2 3 |
)−1 | = | 3 2 |
Example 9. Use the rules of exponents to evaluate (2−3· 104)−2.
| Solution. | (2−3· 104)−2 | = | 26· 10−8 | Power of a power |
| = |  |
|||
| = | _64_ 100,000,000 |
|||
Problem 6. Evaluate the following.
| a) | 2−4 | = |
1 24 |
= |
1 16 |
b) | 5−2 | = |
1 52 |
= |
1 25 |
c) | 10−1 | = |
1 101 |
= |
1 10 |
| d) | (−2)−3 | = |
1 (−2)3 |
= |
1 −8 |
= | − |
1 8 |
| e) | (−2)−4 | = |
1 (−2)4 |
= |
1 16 |
f) | −2−4 | = | − |
1 24 |
= | − |
1 16 |
g) (½)−1 = 2. 2 is the reciprocal of ½.
Problem 7. Use the rules of exponents to evaluate the following.
| a) | 10²· 10−4 = 102 − 4 = 10−2 = 1/100. |
| b) | (2−3)² | = | 2−6 | = | 1 26 |
= |
1 64 |
| c) | (3−2· 24)−2 | = | 34· 2−8 | = |
34 28 |
= |
81 256 |
| d) | 2−2· 2 | = | 2−2+1 | = | 2−1 | = |
1 2 |
Problem 8. Rewrite without a denominator.
| a) | x² x5 |
= | x2−5 | = | x−3 | b) | y y6 |
= | y1−6 | = | y−5 |
| c) |  |
= | x−3y−4 | d) |  |
= | a−1b−6c−7 |
| e) | 1 x |
= | x−1 | f) | 1 x3 |
= | x−3 |
| g) | (x + 1) x |
= | (x + 1)x−1 | h) | (x + 2)2 (x + 2)6 |
= | (x + 2)−4 |
Example 10. Rewrite without a denominator and evaluate:
Answer. The rule for subtracting exponents --
-- holds even when an exponent is negative.
Therefore,
|
= | 10−3 + 5 − 2 + 4 | = | 104 | = | 10,000. |
Exponent 2 goes into the numerator as −2; exponent −4 goes there as +4.
Problem 9. Rewrite without a denominator and evaluate.
| a) | 2² 2−3 |
= 22 + 3 = 25 = 32 | b) | 10² 10−2 |
= 102 + 2 = 104 = 10,000 |
| c) |  |
= 102 − 5 − 4 + 6 = 10−1 = | 1 10 |
| d) |  |
= 25 − 6 + 9 − 7 = 21 = 2 |
The reciprocal of a−n.
Reciprocals come in pairs. The reciprocal of an is a−n :
| 1 an |
= | a−n | . |
And the reciprocal of a−n is an :
| 1 a−n |
= | an | . |
That implies:
Factors may be shifted between the denominator and the numerator
by changing the sign of the exponent.
| Example 11. Rewrite without a denominator: |  |
| Answer. |  |
The exponent 3 goes into the numerator as −3; the exponent −4 goes there as +4.
Problem 10. Rewrite with positive exponents only.
| a) | x y−2 |
= | xy² | b) |  |
= |  |
c) |  |
= |  |
| d) |  |
= |  |
e) |  |
= |  |
Problem 11. Apply the rules of exponents, then rewrite with positve exponents.
| a) |  |
= |  |
= |  |
b) |  |
= |  |
= |  |
Next Lesson: Multiplying and dividing algebraic fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2010 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com