Lesson 4
MULTIPLYING AND DIVIDING
BY POWERS OF 10
The Meaning of Percent
The Metric System
Thanks to our system of positional numeration, it is a simple matter to multiply or divide by a power of 10. It never calls for the written methods we use with other numbers (Lesson 9). And it certainly does not call for a calculator. For the remainder of this course, multiplying and dividing by powers of 10 will be a basic skill.
In this Lesson, we will answer the following:
- How do we multiply a whole number by a power of 10?
- How do we multiply a decimal by a power of 10?
- How do we divide a decimal by a power of 10?
- How do we divide a whole number by a power of 10?
- What does "percent" mean?
- How can we take 1% of a number?
- How can we take 10% of a number?
- How do we change a percent to a number?
- How do we change a number to a percent?
- When is a number written in "scientific notation"?
- What is the metric system?
- How do we convert units in the metric system?
| 1. | How do we multiply a whole number by a power of 10? |
| 36 × 10 | |
| Add on as many 0's as appear in the power. | |
| Examples. | 36 × 10 | = | 360 | Add on one 0. | |
| 36 × 100 | = | 3600 | Add on two 0's. | ||
| 36 × 1000 | = | 36,000 | Add on three 0's. |
Doing that is an example of skill in arithmetic, which is to be able to do a problem as quickly and as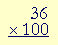 
easily as possible. Traditional multiplication would eventually give the right answer (we hope). But it is not skillful, and it does not take advantage of positional numeration. The student should let go of that written method immediately.
| 2. | How do we multiply a decimal by a power of 10? |
| 7.32 × 10 | |
| Move the decimal point right as many places as there are 0's in the power. If there are not enough digits, add on 0's. |
|
Examples.
| 7.32 × 10 | = 73.2 | Move the decimal point one place right. |
| 7.32 × 100 | = 732 | Move the point two digits right: 732. However, since all the digits fall to the left of the decimal point, the answer is a whole number, 732, which we write without a decimal point. |
| 7.32 × 1000 | = 7,320 | Move the point three digits right. To do this,
we must add on a 0. Again, the answer is a whole number. |
Problem. If 5 pounds of sugar cost $2.79, how much will 50 pounds cost?
Answer. Since 50 pounds are ten times 5 pounds, they will cost ten times more. Move the decimal point one place right: $27.90. Since money has two decimal digits, we added on a 0. (Lesson 3, Question 8)
| 3. | How do we divide a decimal by a power of 10? |
| 63.4 ÷ 10 | |
| "63.4 divided by 10." | |
| Move the decimal point left as many places as there are 0's in the power. If there are not enough digits, add on 0's. | |
| Examples. | 63.4 ÷ 10 | = | 6.34 | Move the point one place left. |
| 63.4 ÷ 100 | = | .634 | Move the point two digits left. | |
| 63.4 ÷ 1000 | = | .0634 | Move the point three digits left. To do this, add on a 0. |
These example illustrate that, whenever we multiply or divide
by a power of 10, the digits do not change
We simply move the decimal point
or add on 0's.
Finally, we must see how to divide a whole number by a power of 10. Now in Lesson 2 we saw that when a whole number ends in 0's, we simply take off 0's. (Lesson 2, Question 10)
265,000 ÷ 100 = 2,650
But when a whole number does not end in 0's -- as 265 -- then
there are no 0's to chop off We will see that we must place a decimal point to
separate digits on the right.
| 4. | How do we divide a whole number by a power of 10? |
| 265 ÷ 10 | |
| Starting from the right of the whole number, separate as
many decimal digits as
there are 0's in the power. If there are not enough digits, add on 0's. |
|
Examples.
| 265 ÷ 10 | = 26.5 | Starting from the right of 265, separate one decimal digit. |
| 265 ÷ 100 | = 2.65 | Separate two decimal digits. |
| 265 ÷ 1000 | = .265 | Separate three decimal digits. |
When we divide a whole number by a power of 10, the answer will have as many decimal digits are there are 0's.
8 ÷ 100 = .08
Two 0's. Two decimal digits.
Again, as in Lesson 2, consider this array:
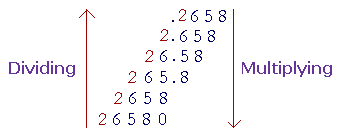
As we move up the list -- as we push the digits one place right -- the number has been divided by 10 because each place to the right is worth 10 times less. (As we move from 26.58 to 2.658, we go from 2 tens to 2 ones.) It appears, though, as if the decimal point has shifted one place left, or, with the whole number 26580, that a 0 has been taken off.
As we move down the list -- as we push the digits to the left through the decimal point -- each number has been multiplied by 10.
And so we can easily multiply or divide by a power of 10 because of our system of positional numeration. Each place belongs to the next power of 10.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2: The meaning of percent
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com