9
INSTANTANEOUS VELOCITY
AND
RELATED RATES
The definition of instantaneous velocity
ONE OF THE most important applications of calculus is to motion in a straight line, which is called rectilinear motion.

Consider a particle moving in a straight line from a fixed point O to a given point P, and let t be the time elapsed. Then to each value of t there will correspond a distance s, which will be a function of t:
s = s(t).
When we know s(t), we have what is called the equation of motion.
Now, if the particle moves with constant velocity—which is called uniform motion—then we don't need calculus. In other words, if the equation of motion is
s = 22 t,
then at every instant of time, the velocity, v(t), is 22 m/sec. For the slope of that line—22—is rate of change of s with respect to t, which by definition is the velocity.
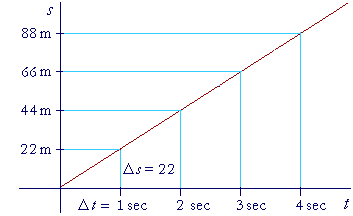
In each 1 second of time, the particle moves a distance of 22 meters.
| Δs Δt |
= | 22 meters per second. |
That is not a realistic picture, of course, because at 0 seconds the velocity is surely not 22 meters/sec. There must have been an acceleration
to that constant velocity. During that acceleration, the velocity was not constant. The graph was not a straight line.
The definition of instantaneous velocity
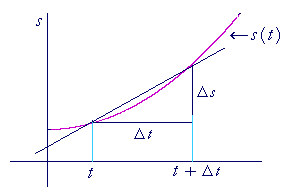
For any equation of motion s(t), by the instantaneous velocity at time t—v(t)—we mean the limit of the average velocity, ![]() , between t and t + Δt, as Δt approaches 0.
, between t and t + Δt, as Δt approaches 0.
![]()
The instantaneous velocity is the value of the slope of the tangent line at t.
Example 1. Let the following be the equation of motion:
s(t) = 6t 2 + t + 8.
Let t be measured in minutes and s in meters. And let 10:05 AM correspond to t = 0.
a) What is the instantaneous velocity at 10:05 AM?
| Answer. | ds dt |
= | 12t + 1 |
| = | 12· 0 + 1 | ||
| = | 1 m/min. | ||
b) What is the instantaneous velocity at 10:15 AM?
Answer. At 10:15, t = 10.
| ds dt |
= | 12· 10 + 1 |
| = | 121 m/min. | |
Instantaneous velocity is not an ordinary velocity. It is the limit of a sequence of velocities as Δt approaches 0; it is purely logical; it can never be observed or measured. To measure a velocity, it is necessary to know both a distance Δs and a time Δt, however small.
A body in motion is in motion during every interval of time in which it moves. If we say at every instant of time—and assume that time is composed of instants—then we invite the arrow paradox of Zeno. At any one instant, he argued, there is no interval of time, hence there is no change of position; which means: no motion.
The definition of instantaneous velocity does not imply that time is composed of instants. It specifies how to evaluate that velocity at any specific time t that we name. Which is all that we require, and all that we ever do.
See the Appendix, Is a line really composed of points.
Problem 1. It has been found by experiment that a body falling from rest under the influence of gravity, follows approximately this equation of motion:
s(t) = 4.9 t 2.
s is the distance fallen measured in meters; t is the time elapsed measured in seconds.
a) At the end of 3 seconds, how far has the body fallen?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
s(3) = 4.9 × 32 = 4.9 × 9 = 44.1 m.
b) What is its instantaneous velocity at the end of 3 seconds?
| ds dt |
= | 9.8 t |
| = | 9.8 × 3 | |
| = | 29.4 m/sec. | |
The second derivative
The derivative of y = f(x)—y'(x)— will itself be a function of x. That new function may itself be differentiable. If that is the case, we call the derivative of the first derivative of y the second derivative. The notation
| for the second derivative is | or y''. |
Consider this equation of motion,
s(t) = 3t 2.
Then the first derivative is the velocity v:
| v = | ds dt |
= 6t. |
The second derivative is the rate of change of the velocity with respect to time. That is called the acceleration a:
| a = | d2s dt2 |
= 6. |
If t is measured in seconds and s in meters, then the units of velocity are meters per second, which we abbreviate as m/sec. The units of acceleration are then meters per second per second, which we abbreviate as m/sec2.
Problem 2. A body moves in a straight line according to this equation of motion:
s(t) = 10t 2 − 4t + 8,
where t is measured in seconds and s in meters.
a) What is its position at the end of 5 sec?
s(5) = 10· 52 − 4· 5 + 8 = 238 m.
b) What is the equation for its velocity v at any time t ?
| v(t) = | ds dt |
= 20t − 4. |
c) What is its velocity v at the end of 5 seconds?
v(5) = 20· 5 − 4 = 96 m/sec.
d) What is the equation for its acceleration a at any time t ?
| a(t) = | d2s dt2 |
= | dv dt |
= 20. |
e) What is its acceleration at the end of 5 seconds?
a(5) = 20 m/sec2.
The acceleration is constant.
Problem 3. Under the influence of gravity, a body moves according to this equation of motion:
s(t) = ½gt 2 + s0
a) What is the physical significance of the constant s0?
It is the body's initial position, s(0).
b) How fast is the body moving after 5 seconds?
| v(t) = | ds dt |
= gt. At t = 5, v(5) = 5g. |
c) What is the physical significance of the constant g?
| g = | d2s dt2 |
. g is the acceleration due to gravity, which is |
approximately 9.8 m/sec2.
Example 2.
a) If the radius of a circle is expanding, write the equation that shows
a) how fast the area of the circle is expanding. (A = πr2.)
| Solution. We are to calculate | dA dt |
. We have |
| A | = | πr2. | ||
| On differentiating implicitly with respect to t: | ||||
| dA dt |
= | = | ||
b) If the radius is expanding at the rate of 2 cm/min, how fast is the
a) area expanding when the radius is 15 cm?
| Solution. We are given that | dr dt |
= 2 cm/min. Therefore, |
when r = 15 cm:
| dA dt |
= | 2π· 15· 2 |
| 188.4 cm2/min. |
Example 3. A boy is walking at the rate of 5 miles per hour toward the foot of a flag pole 60 feet high. At what rate is his distance from the top of the pole changing when he is 80 feet from its foot?
Solution. Draw a picture![]() In all problems of this type, draw a picture.
In all problems of this type, draw a picture.
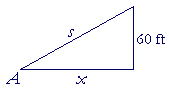
Let the boy be at the point A, which is a distance x from the foot of the flag pole. Let s be his distance from the top of the pole.
| We are to calculate | ds dt |
. |
The figure is a right triangle. Therefore,
| 1) | s2 = x2 + 3600. |
Differentiate implicitly with respect to t.
| 2s | ds dt |
= | 2x | dx dt |
. |
Therefore,
| ds dt |
= | x s |
dx dt |
. |
| Now, we are given x = 80 feet, and | dx dt |
= −5 mi/hour. We |
write the minus sign because x is decreasing as he approaches the flag pole.
According to line 1),
![]()
Therefore,
Problem 4. The side of a square is a cm long, and is increasing at the rate of b cm per hour. How fast is the area increasing?
2ab cm2/hour.
Problem 5. The side of an equilateral triangle is a cm long, and is increasing at the rate of b cm per hour. How fast is the area increasing?
½ab ![]() cm2/hour.
cm2/hour.
Problem 6.
a) The surface area S of a sphere is given by the formula S = 4πr2.
If r changes with time, how does S change?
| dS dt |
= | 8πr | dr dt |
b) The volume V of a sphere is given by the formula V =
![]() πr3.
πr3.
If r changes with time, how does V change?
| dV dt |
= | 4πr2 | dr dt |
| c) Prove: | dV dt |
= | ½r | dS dt |
. |
| dV dt |
= | 4πr2 | dr dt |
= ½· 8πr2 | dr dt |
= ½r· 8πr | dr dt |
= ½r | dS dt |
. |
Problem 7. The base and height of a rectangle are b and h, and they are changing at the rates p, q respectively. Prove that the area A is changing at the rate bq + hp.
A = bh.
According to the product rule:
| dA dt |
= | b | dh dt |
+ | h | db dt |
= | bq + hp. |
Problem 8.
a) A ladder 50 feet long is leaning against a wall. If the foot of the
a) ladder is being pulled away from the wall at a certain rate, derive the
a) formula for how fast the top of the ladder is descending.
a) (Let x be the distance of the foot of the ladder from the wall,
a) and let h be the distance of the top from the ground. Draw a
a) picture![]() )
)
| dh dt |
= − | x h |
dx dt |
= | 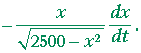 |
b) If the foot is being pulled away at the rate of 3 ft/min:
1) how fast is the top descending when the foot is 14 feet from the
1) wall?
7/8 ft/min.
2) when is the top descending at the rate of 4 ft/min?
When the bottom is 40 feet from the wall.
c) When will the top and bottom move at the same rate?
When the bottom is 25![]() feet from the wall.
feet from the wall.
![]()
Next Lesson: Maximum and minimum values
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
