1
The Formal Rules of Algebra
The student who has had a course in algebra, will find this a complete review. The student who is now taking such a course, will see what is in store.
ALGEBRA is a method of written calculations. And what is a calculation but replacing one set of symbols with another? In arithmetic we replace '2 + 2' with '4.' In algebra we may replace 'a + (−b)' with 'a − b.'
a + (−b) = a − b.
We call that a formal rule. It shows how an expression written in one form may be replaced with a different form. The = sign means "may be rewritten as" or "may be replaced by."
If p and q are statements (equations), then a rule
If p, then q,
or equivalently
p implies q,
means: We may replace—in the sense of follow—statement p with statement q. For example,
x + a = b implies x = b − a.
That means that we may follow the statement 'x + a = b' with the statement 'x = b − a.'
For we solve equations by a logical sequence of statements.
Algebra depends on how things look. We can say, then, that algebra is a system of formal—grammatical—rules. What follows are what we are permitted to write.
(See the complete course, Skill in Algebra.)
11. The axioms of "equals"
| a = a | Identity | |
| If a = b, then b = a. | Symmetry | |
| If a = b and b = c, then a = c. | Transitivity | |
It is not possible to give an explicit definition of the word "equals," or its symbol = . Those rules however are an implicit definition. The meaning of "equals" implies those three rules.
As for how the rule of symmetry comes up in practice, see Lesson 6 of Algebra. The rule of symmetry applies to all of the rules below.
12. The commutative rules of addition and multiplication
| a + b | = | b + a |
| a· b | = | b· a |
13. The identity elements of addition and multiplication:
3. 0 and 1
a + 0 = 0 + a = a
a· 1 = 1· a = a
Thus, if we "operate" on a number with an identity element,
it returns that number unchanged.
14. The additive inverse of a: −a
a + (−a) = −a + a = 0
The "inverse" of a number undoes what the number does.
For example, if you start with 5 and add 2, then to get back to 5 you must add −2. Adding 2 + (−2) is then the same as adding 0 -- which is the identity.
| 15. The multiplicative inverse or reciprocal of a, | ||
| 5. symbolized as | 1 a |
(a |
| a· | 1 a |
= | 1 a |
· a | = 1. |
Two numbers are called reciprocals of one another if their product is 1.
Thus, 1/a symbolizes that number which, when multiplied by a, produces 1.
| The reciprocal of | p q |
is | q p |
. |
16. The algebraic definition of subtraction
a − b = a + (−b)
Subtraction, in algebra, is defined as addition of the inverse.
17. The algebraic definition of division
| a b |
= | a· | 1 b |
Division, in algebra, is defined as multiplication by the reciprocal.
Hence, algebra has two fundamental operations: addition and multiplication.
18. The inverse of the inverse
−(−a) = a
19. The relationship of b − a to a − b
b − a = −(a − b)
Now, b + a is equal to a + b. But b − a is the negative of a − b.
10. The Rule of Signs for multiplication, division, and
10. fractions
a(−b) = −ab. (−a)b = −ab. (−a)(−b) = ab.
| a −b |
= − | a b |
. | −a b |
= − | a b |
. | −a −b |
= | a b |
. |
"Like signs produce a positive number; unlike signs, a negative number."
11. Rules for 0
a· 0 = 0· a = 0.
If a ![]() 0, then
0, then
| 0 a |
= 0. | a 0 |
= No value. | 0 0 |
= Indeterminate. |
Division by 0 is an excluded operation. (Skill in Algebra, Lesson 5.)
| m(a + b) = ma + mb | The distributive rule/ | |
| Common factor | ||
| (x − a)(x − b) = x2 − (a + b)x + ab | ||
| Quadratic trinomial | ||
| (a ± b)2 = a2 ± 2ab + b2 | Perfect square trinomial | |
| (a + b)(a − b) = a2 − b2 | The difference of | |
| two squares | ||
| (a ± b)(a2 |
The sum or difference of | |
| two cubes | ||
13. The same operation on both sides of an equation
| If | If | |||||||
| a | = | b, | a | = | b, | |||
| then | then | |||||||
| a + c | = | b + c. | ac | = | bc. | |||
We may add the same number to both sides of an equation;
we may multiply both sides by the same number.
14. Change of sign on both sides of an equation
| If | |||
| −a | = | b, | |
| then | |||
| a | = | −b. | |
We may change every sign on both sides of an equation.
15. Change of sign on both sides of an inequality:
15. Change of sense
| If | |||
| a | < | b, | |
| then | |||
| −a | > | −b. | |
When we change the signs on both sides of an inequality, we must change the sense of the inequality.
16. The Four Forms of Equations corresponding to the
16. Four Operations and their inverses
| If | If | |||||||
| x + a | = | b, | x − a | = | b, | |||
| then | then | |||||||
| x | = | b − a. | x | = | a + b. | |||
| * | * | * |
| If | If | |||||||
| ax | = | b, | x a |
= | b, | |||
| then | then | |||||||
| x | = | b a |
. | x | = | ab. | ||
See Skill in Algebra, Lesson 9.
17. Change of sense when solving an inequality
| If | ||||
| −ax | < b, | |||
| then | ||||
| x | > − | b a |
. | |
18. Absolute value
If |x| = b, then x = b or x = −b.
If |x| < b then −b < x < b.
If |x| > b (and b > 0), then x > b or x < −b.
19. The principle of equivalent fractions
| x y |
= | ax ay |
|
| and symmetrically, | |||
| ax ay |
= | x y |
|
We may multiply both the numerator and denominator by the same factor; we may divide both by a common factor.
20. Multiplication of fractions
| a b |
· | c d |
= | ac bd |
| a · | c d |
= | ac d |
|
21. Division of fractions (Complex fractions)
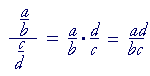
Division is multiplication by the reciprocal.
22. Addition of fractions
| a c |
+ | b c |
= | a + b c |
Same denominator |
| a b |
+ | c d |
= | ad + bc bd |
Different denominators with no common factors |
| a bc |
+ | e cd |
= | ad + be bcd |
Different denominators with common factors |
The common denominator is the LCM of denominators.
23. The rules of exponents
| aman | = | am+n | Multiplying or dividing | |
| am an |
= | am−n | powers of the same base |
|
| (ab)n | = | anbn | Power of a product of factors | |
| (am)n | = | amn | Power of a power | |
24. The definition of a negative exponent
| a−n | = | 1 an |
25. The definition of exponent 0
a0 = 1
26. The definition of the square root radical
![]()
The square root radical squared produces the radicand.
27. Equations of the form a2 = b
| If | |||
| a2 | = | b, | |
| then | |||
| a | = | ± |
|
28. Multiplying/Factoring radicals
| = | |||
| and symmetrically, | |||
| = | |||
29. The definition of the nth root
![]()
30. The definition of a rational exponent
![]()
It is more skillfull to take the root first.
31. The laws of logarithms
log xy = log x + log y.
| log | x y |
= log x − log y. |
log xn = n log x.
| log 1 = 0. | logbb = 1. |
32. The definition of the complex unit i
i 2 = −1
Next Topic: Rational and irrational numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
