6
Definitions of the Trigonometric Functions
of an Acute Angle
BEFORE DEFINING THE TRIGONOMETRIC FUNCTIONS, we must see how to relate the angles and sides of a right triangle.
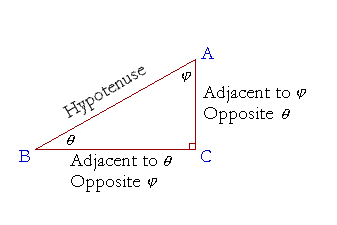
A right triangle is composed of a right angle, the angle at C, and two acute angles, which are angles less than a right angle. It is conventional to label the acute angles with Greek letters. We will label the angle at B with the letter θ ("THAY-ta"). And we will label the angle at A with the letter φ ("fie").
As for the sides, the side AB, opposite the right angle, is called the hypotenuse ("hy-POT'n-yoos"). Each acute angle is formed by the hypotenuse and the side adjacent to the angle. Angle θ is thus formed by the hypotenuse and side BC. Angle φ is formed by the hypotenuse and side AC.
With respect to angle θ, though, side AC is its opposite side. While side BC is the side opposite φ.
The ratios of sides
Any two sides of the triangle will have a ratio -- a relationship -- to one another. It is possible to form six such ratios: the opposite side to the hypotenuse; the adjacent side to the opposite; and so on. Those six ratios have historical names and abbreviations, with which the student will have to make peace. They are the following.
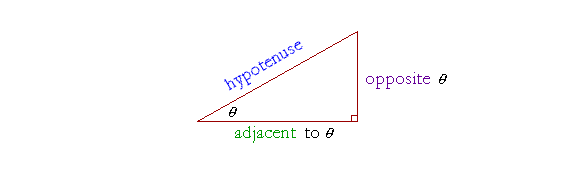
| sine of θ | = | sin θ | = | opposite hypotenuse |
cosecant of θ | = | csc θ | = | hypotenuse opposite |
|
| cosine of θ | = | cos θ | = | adjacent hypotenuse |
secant of θ | = | sec θ | = | hypotenuse adjacent |
|
| tangent of θ | = | tan θ | = | opposite adjacent |
cotangent of θ | = | cot θ | = | adjacent opposite |
|
Notice that each ratio in the right-hand column is the reciprocal of the ratio in the left-hand column.
The reciprocal of sin θ is csc θ ; and vice-versa.
The reciprocal of cos θ is sec θ.
And the reciprocal of tan θ is cot θ.
We will see in the next Topic that the value of each ratio depends only on the value of the acute angle. Therefore we say that each ratio is a function of the acute angle. Hence we call the six ratios the trigonometric functions of an acute angle. All of trigonometry is based on the definitions of those functions.
Problem 1. Complete the following with either "opposite," "adjacent to," or "hypotenuse."
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
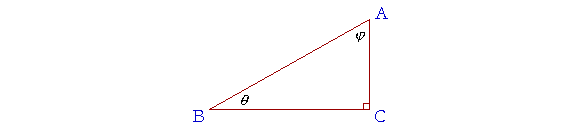
a) In a right triangle, the side opposite the right angle is called the
a) hypotenuse.
b) CA is called the side opposite angle θ.
c) BC is called the side adjacent to angle θ.
d) AC is called the side adjacent to angle φ.
e) BC is called the side opposite angle φ.
Problem 2. The sides of a right triangle are in the ratio 3 : 4 : 5, as shown. Name and evaluate the six trigonometric functions of angle θ.
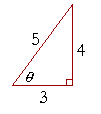
| sin θ | = | 4 5 |
csc θ | = | 5 4 |
| cos θ | = | 3 5 |
sec θ | = | 5 3 |
| tan θ | = | 4 3 |
cot θ | = | 3 4 |
Problem 3. The sides of a right triangle are in the ratio 8 : 15 : 17, as shown. Name and evaluate the six trigonometric functions of angle φ.

| sin φ | = | 15 17 |
csc φ | = | 17 15 |
| cos φ | = | 8 17 |
sec φ | = | 17 8 |
| tan φ | = | 15 8 |
cot φ | = | 8 15 |
Notice that the sides of this triangle satisfy, as they must, the Pythagorean theorem:
| 82 + 152 | = | 172 |
| 64 + 225 | = | 289 |
Problem 4. A straight line makes an angle θ with the x-axis. The value
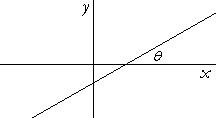
of which function of θ is equal to its slope?
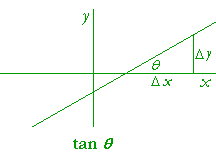
Two theorems.
Theorem 1. The area of a triangle. The area of a triangle is equal to one-half the sine of any angle times the product of the two sides that make the angle.
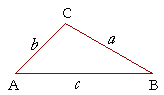
Specifically:
Area of triangle ABC = ½ sin A bc = ½ cb sin A.
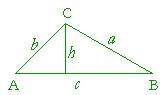
The area of a triangle is equal to one-half the base times the height. In triangle ABC, let the base be c and the height h. Then
Area = ½ ch.
Now,
sin A = h/b,
so that
h = b sin A.
Therefore in the expression for the Area, replace h with b sin A:
Area = ½ cb sin A.
Which is what we wanted to prove.
Theorem 2. The ratio of the areas of similar triangles.
Similar triangles are to one another as the squares drawn
on their corresponding sides.
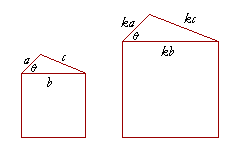
When triangles are similar, then by whatever factor side a changes, sides b and c will change by that same factor. Proportionally,
![]()
Therefore, according to Theorem 1, the area of the triangle on the left has the following ratio to the triangle on the right:
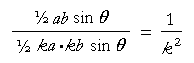
But the areas of the squares on the corresponding sides have that same ratio.
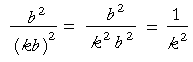
Therefore, similar triangles are to one another as the squares drawn on their corresponding sides.
Which is what we wanted to prove.
Next Topic: Trigonometry of right triangles
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com