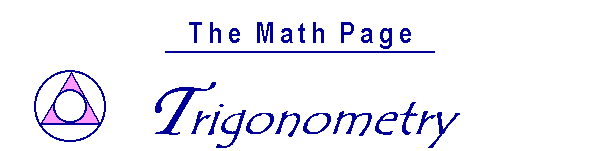
11
THE LAW OF COSINES
WE USE THE LAW OF COSINES AND THE LAW OF SINES to solve triangles that are not right-angled. Such triangles are called oblique triangles. The Law of Cosines is used much more widely than the Law of Sines. Specifically, when we know two sides of a triangle and their included angle, then the Law of Cosines enables us to find the third side.
Thus if we know sides a and b and their included angle θ, then the Law of Cosines states:
c2 = a2 + b2 − 2ab cos θ
(The Law of Cosines is a extension of the Pythagorean theorem, because if θ were a right angle, we would have c2 = a2 + b2.)
Example 1. In triangle DEF, side e = 8 cm, f = 10 cm, and the angle at D is 60°. Find side d.
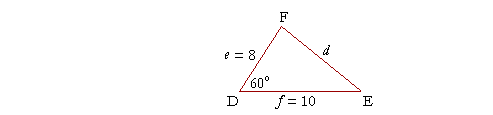
Solution.. We know two sides and their included angle. Therefore, according to the Law of Cosines:
d2 = e2 + f2 − 2ef cos 60°
d2 = 82 + 102 − 2· 8· 10· ½, since cos 60° = ½,
d2 = 164 − 80
d2 = 84.
d = 
.
Problem 1. In the oblique triangle ABC, find side b if side a = 5 cm, c = 
cm, and they include and angle of 45°. No Tables.
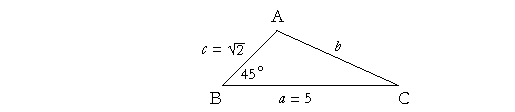
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
b2 = a2 + c2 − 2ac cos 45°
= 52 + (
)2 − 2· 5· · cos 45°
= 25 + 2 − 10· ·
½, since cos 45° = ½,
= 25 + 2 − 10, (· = 2)
= 17.
b
= 
cm.
Problem 2. In the oblique triangle PQR, find side r if side p = 5 in, q = 10 in, and they include and angle of 14°. (Table)
r2 = 52 + 102 − 2· 5· 10 cos 14°
= 25 + 100 − 100(.970), from the Table.
= 125 − 97
= 28.
r = 
in.
Example 2. In Example 1, we found that d = , which is approximately 9.17.
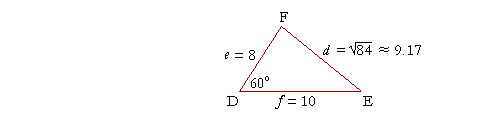
Use the Law of Sines to complete the solution of triangle DEF. That is, find angles E and F.
| Solution. To find angle F, we have this version of | Unknown Known |
: |
| sin F sin D |
= | f d |
||
| sin F sin 60° |
= | 10 9.17 |
||
| sin F | = | (.866) | 10 9.17 |
from the Table, |
 |
.944 | with the aid of a calculator. | ||
Therefore, on inspecting the Table for the angle whose sine is closest to .944,
Angle F 71°.
And therefore,
| Angle E | = | 180° − (71° + 60°) |
| = | 180° − 131° | |
| = | 49°. | |
And so using the Laws of Sines and Cosines, we have completely solved the triangle.
The Law of Cosines is also valid when the included angle is obtuse. But in that case, the cosine is negative. See Topic 16.
Proof of the Law of Cosines
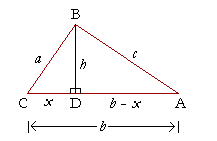
Let ABC be a triangle with sides a, b, c. We will show
c2 = a2 + b2 − 2ab cos C.
(The trigonometric functions are defined in terms of a right-angled triangle. Therefore it is only with the aid of right-angled triangles that we can prove anything
)
Draw BD perpendicular to CA, separating triangle ABC into the two right triangles BDC, BDA. BD is the height h of triangle ABC.
Call CD x. Then DA is the whole b minus the segment x: b − x.
Also, since
| x a |
= cos C, |
then
x = a cos C . . . . . . . (1)
Now, in the right triangle BDC, according to the Pythagorean theorem,
h2 + x2 = a2,
so that
h2 = a2 − x2. . . . . . (2)
In the right triangle BDA,
c2 = h2 + (b − x)2
c2 = h2 + b2 − 2bx + x2.
For h2, let us substitute line (2):
c2 = a2 − x2 + b2 − 2bx + x2
c2 = a2 + b2 − 2bx.
Finally, for x, let us substitute line (1):
c2 = a2 + b2 − 2b· a cos C.
That is,
c2 = a2 + b2 − 2ab cos C.
This is what we wanted to prove.
In the same way, we could prove that
a2 = b2 + c2 − 2bc cos A
and
b2 = a2 + c2 − 2ac cos B.
This is the Law of Cosines.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com