Lesson 22, Section 2
Complex fractions -- Division
| A complex fraction looks like this: |
The numerator and/or the denominator are themselves fractions.
To simplify a complex fraction, we can immediately apply the definition of division (Lesson 6):
| a b |
= a · | 1 b |
Any fraction is equal to the numerator times the reciprocal
of the denominator.
Therefore,
| = | p q |
· | n m |
Problem 1. State in words how to simplify a complex fraction.
Rewrite it as the numerator times the reciprocal
of the denominator.
| Example 1. Simplify | 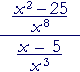 |
| Solution. | 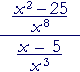 |
= | x2 − 25 x8 |
· | x³ x − 5 |
| = | (x + 5)(x − 5) x8 |
· | x³ x − 5 |
|
| = | x + 5 x5 |
|||
Division -- which effectively this is -- becomes multiplication by the reciprocal.
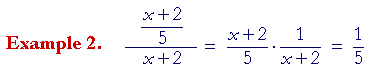
on canceling the x + 2's.
Problem 2. Simplify.
| a) | = |
6 x5 |
· |
x2 8 |
= |
3 4x3 |
| b) | 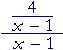 |
= |
4 x − 1 |
· |
1 x − 1 |
= |
_4_ x2 − 2x + 1 |
| c) | 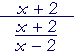 |
= | (x + 2) | · |
x − 2 x + 2 |
= | x − 2 |
| d) | 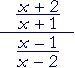 |
= |
x + 2 x + 1 |
· |
x − 2 x − 1 |
= |
x2 − 4 x2 − 1 |
| e) | 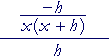 |
= |
−h x(x + h) |
· |
1 h |
= | − |
1 x(x + h) |
The h's cancel. And according to the Rule of Signs, the product is negative. (It's all right to leave the product in its factored form.)
| f) | 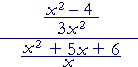 |
= |
(x + 2)(x − 2) 3x2 |
· |
_x_ (x + 2)(x + 3) |
| = |
x − 2 3x |
· |
1 x + 3 |
= |
x − 2 3x(x + 3) |
Example 3. If a complex fraction looks like this --
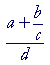
-- then we can simplify it by multiplying the numerator and denominator by c.
![]()
Problem 3. Simplify the following.
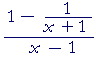 |
= | _(x + 1) − 1_ (x + 1)(x − 1) |
= | __x__ x2 − 1 |
| Example 4. Simplify | |
Solution. 1-over any number is its reciprocal. Therefore,
| = | 4 3 |
Problem 4. Simplify the following.
| a) | 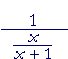 |
= | x + 1 x |
b) | 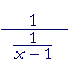 |
= | x − 1 |
Next Lesson: Adding algebraic fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
