4
MULTIPLYING AND DIVIDING
SIGNED NUMBERS
We can only do arithmetic in the usual way. To calculate 5(−2), we have to do 5 · 2 = 10 -- and then decide on the sign. Is it +10 or −10? For the answer, we have the followng Rule of Signs.
1. What is the Rule of Signs for multiplying, dividing, and
fractions?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Like signs produce a positive number;
unlike signs, a negative number.
| Example 1. | −5(−2) | = | 10. | Like signs. |
| 5(−2) | = | −10. | Unlike signs. | |
| −12 −4 |
= | 3. | Like signs. | |
| 12 −4 |
= | −3. | Unlike signs. | |
For an explaination of these rules, see below.
2. Write the formal Rule of Signs as it applies to fractions.
| −a −b |
= | a b |
−a b |
= − | a b |
a −b |
= − | a b |
A formal rule is simply a rule we write with letters. We write it with letters because we want it to apply to any numbers. We want it to apply to whatever looks like that.
| Example 2. | −2 −6 |
= | 1 3 |
|
| −2 6 |
= | − | 1 3 |
|
| 1 −3 |
= | − | 1 3 |
|
Problem 1. Calculate the following.
| a) | 7(−8) = −56 | b) | (−7)8 = −56 | c) | 8(−7) = −56 | d) | −8(−7) = 56 | |||
| e) | (−3)7 = −21 | f) | 5(−9) = −45 | g) | −6(−9) = 54 | h) | −8(−4) = 32 | |||
Problem 2. Evaluate the following. (Be careful to distinguish the operations.)
| a) | 4 − 6 = −2 | b) | 4(−6) = −24 | |
| c) | (−4) − 6 = −10 | d) | (−4)(−6) = 24 | |
| e) | 5 − 8 · 2 = −11 | f) | (5 − 8) · 2 = −6 | |
| g) | 5 − 8 + 2 = −1 | h) | 5 − (8 + 2) = −5 | |
| i) | 2 − 3(−6) = 20 | j) | (2 − 3)(−6) = 6 | |
Example 3. The form a − b(−c). Consider a problem in this form:
3 − 5(−2).
We are to subtract 5 times −2:
| 3 − 5(−2) | = | 3 − (−10) |
| = | 3 + 10 | |
| = | 13. | |
And so even though the problem means to subtract (5 times −2), we may interpret it to mean: −5 times −2 = +10. We may simply write
| 3 − 5(−2) | = | 3 + 10 |
| = | 13. | |
In other words, any problem that looks like this --
a − b(−c)
-- we may evaluate like this:
a + bc.
Problem 3. Evaluate the following.
| a) | 8 − 2(−4) = 8 + 8 = 16 | b) | 9 − 5(−2) = 9 + 10 = 19 | |
| c) | −20 − 3(−5) = −5 | d) | −70 − 9(−7) = −7 | |
| e) | 3 + 4(−9) = −33 | f) | −6 + 5(−2) = −16 | |
| g) | −10 − 2(4 −8) = −2 | h) | (−10 − 2)(4 −8) = (−12)(−4) = 48 | |
Problem 4. Two variables. Let the value of y depend on the value
of x as follows:
y = 3x − 6.
Calculate the value of y that corresponds to each value of x:
When x = 0, y = 3 · 0 − 6 = 0 − 6 = −6.
When x = 1, y = 3 · 1 − 6 = 3 − 6 = −3 .
When x = −1, y = 3 · −1 − 6 = −3 − 6 = −9.
When x = 2, y = 3 · 2 − 6 = 6 − 6 = 0.
When x = −2, y = 3 · −2 − 6 = −6 − 6 = −12.
When x = 3, y = 3 · 3 − 6 = 9 − 6 = 3.
When x = −3, y = 3 · −3 − 6 = −9 − 6 = −15.
Problem 5. Negative factors.
| a) | (−2)(−2) = 4 | b) | (−2)(−2)(−2) = 4(−2) = −8 |
| c) | (−2)(−2)(−2)(−2) = (−8)(−2) = 16 |
| d) | (−2)(−2)(−2)(−2)(−2) = −32 |
Problem 6. According to the previous problem:
An even number of negative factors produces a positive number. While an odd number of negative factors produces a negative number.
Example 4. Multiply −2(−9)7(−5).
Solution. Before even multiplying, we can see that because there are an odd number of negative factors, the sign will be negative.
−2(−9)7(−5) = −2 · 9 · 7 · 5.
We have now only to multiply those numbers.
But the order of factors does not matter. (Lesson 1.) The multiplication therefore will be simpler if we first multiply 2 · 5 --
| −2 · 9 · 7 · 5 | = | −2 · 5 · 9 · 7 |
| = | −10 · 63 | |
| = | −630. | |
Multiplication is always simpler if factors will produce 10, or 100, or any power of 10.
Problem 7. Multiply.
| a) | 2(−3)4 = −24 | b) | (−2)3(−4) = 24 | c) | 2(−3 −4) = −14 | ||
| d) | (−3)(−4)(−5) = −60 | e) | (−1)(−2)(−3)(−4) = 24 | ||||
| f) | (−2)8(−5)7 = 560 | g) | 25(−8)(−3)(−4) = −100 · 24 = −2400 | ||||
| h) | (−1)(−1)(−1) = −1 | i) | (−1)(−1)(−1)(−1) = 1 | ||||
Problem 8. Evaluate each of the following as a positive or negative fraction in lowest terms, or as an integer.
| a) | −24 6 |
= − | 4 | b) | 24 −6 |
= − | 4 | c) | −24 −6 |
= | 4 | ||
| d) | 3 −12 |
= − | 1 4 |
e) | −8 −20 |
= | 2 5 |
f) | −18 42 |
= − | 3 7 |
||
| g) | −2 3 |
= − | 2 3 |
h) | 2 −3 |
= − | 2 3 |
i) | −2 −3 |
= | 2 3 |
||
| j) | −12 3 |
= − | 4 | k) | −5 −20 |
= | 1 4 |
l) | 3 −4 |
= − | 3 4 |
||
In summary, here again is the Rule of Signs.
In both multiplication and division:
Like signs produce a positive number;
unlike signs, a negative number.
| Example 5. Multiplying fractions. |
To multiply fractions, multiply the numerators
and multiply the denominators, as in arithmetic.
Observe the Rule of Signs.
Problem 9. Multiply.
| a) | −3 5 |
· | 7 8 |
= |
−21 40 |
= | − |
21 40 |
b) | 1 2 |
· | −x 4 |
= |
−x 8 |
= | − |
x 8 |
| c) | −2 3 |
· | x −8 |
= |
−2x −24 |
= |
x 12 |
d) | x −6 |
· | 3 −5 |
= |
3x 30 |
= |
x 10 |
|||
An explanation of the Rule of Signs
To decide how negative numbers should behave, we are not able to copy arithmetic. Rather, we have to respect the either-or, yes-or-no nature of logic.
For example, the introduction of the word "not" into a statement changes its truth value. If the statement was true, "not" makes it false, and vice-versa. If this statement
Today is Monday
is true, then
Today is not Monday
is false. But if we write
Today is not not Monday,
then that changes its truth value again. That statement is true![]()
Now in algebra we do not have true or false, but we do have the logical equivalent: positive or negative. Thus if the value of x is positive, then the value of −x must be negative, and vice-versa.
And so since we call the positive or negative value of a number its sign, then we can state the following principle:
A minus sign changes the sign of a number.
A minus sign is the logical equivalent of "not." Geometrically, a minus sign reflects a number symmetrically about 0.
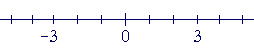
We saw that with −(−3) = 3.
(As for 0, it is best to say that it has both signs: −0 = +0 = 0. See for example Lesson 11, Problem 11.)
If we now apply this principle to multiplication:
A negative factor changes the sign of a product.
Thus if ab is positive, then (−a)b cannot also be positive. It must be negative -- it must be the negative of ab.
(−a)b = −ab.
That is, "Unlike signs produce a negative number."
And upon introducing another negative factor, the sign changes back:
(−a)(−b) = ab.
"Like signs produce a positive number."
This same logical principle will apply to division and fractions. Hence we have the Rule of Signs.
To prove that (−a)b is the negative of ab in what some call a rigorous manner, we would have to apply the definition of the negative of a number. We would have to prove:
ab + (−a)b = 0.
That will be Problem 13 of the Lesson on Common Factor.
Next Lesson: Some rules of algebra
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
