Radicals - Rational and irrational numbers: Level 2
The definition of the square root radical
Example 4. Solve for x:
| (x + 3)² | = | 5. | |
| Solution. All equations fall into certain forms, and this one has the same form as Example 3: |
|||
| z² | = | a. | |
| If an equation looks like that, then the solution will look like this: | |||
| z | = | ± . |
|
In other words, if we call z the argument of the equation z² = a, then in the solution, the argument is on the left. The argument is whatever was squared.
In this equation --
| (x + 3)² | = | 5, | |
| -- the argument is x + 3. Therefore, | |||
| x + 3 | = | ± |
|
| x | = | −3 ± . |
|
Problem 7. Solve for x.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | (x − 1)² | = | 2 | b) | (x + 5)² | = | 6 | |
| x − 1 | = | ± |
x + 5 | = | ± |
|||
| x | = | 1 ± |
x | = | −5 ± |
| c) | (x − p)² | = | q + r |
| x − p | = | ± |
|
| x | = | p ± |
|
The definition of the square root radical
Here is the formal rule that implicitly defines the symbol :
A square root radical multiplied by itself
produces the radicand.
| Example 5. |  · |
= | 2. |
(3a )²
| = | 3²a²()² (Power of a product of factors) |
|
| = | 9a²· 10 | ||
| = | 90a². | ||
Problem 8. Evaluate the following.
| a) |  · = 3 |
b) | ( )² = 5 |
||||
| c) | ( )² = a + b |
d) |  = |
||||
| e) | (5)² = 25· 2 = 50 |
f) | (a4 )² = a8· 3b = 3a8b |
||||
Example 6. Multiply out 
( + ). That is, distribute .
| Solution. | ( + ) |
= | · + · |
| = | 2 + 3 |
||
Problem 9. Following the previous Example, multiply out
( + ).
| ( + ) |
= |  |
| = |  |
|
Rationalizing a denominator
Rationalizing a denominator is a simple technique for changing an irrational denominator into a rational one. We simply multiply the radical by itself. But then we must multiply the numerator by the same number.
| Example 7. Rationalize this denominator: | 1  |
Solution. Multiply both the numerator and denominator by 
:
The denominator is now rational.
 2 |
can also take the form ½: |
2 |
= ½. |
| For, we can write any fraction | a b |
as the numerator times the |
reciprocal of the denominator.
Finally, rationalizing the denominator simplifies the task of evaluating the fraction. Since we know that , for example, is approximately 1.414, then we can easily know that
 |
= ½ ½(1.414) = 0.707. |
| Problem 10. Rationalize the denominator: | 2  |
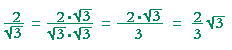
Problem 11. Show each of the following by transforming the left-hand side.
| a) | 6  |
= | 2. |
6  |
= |  3 |
= | 2 |
| b) | 9  |
= |  2 |
9 |
= |  6 |
= |  2 |
| c) |  |
 |
= |  ab |
= |  b |
Real numbers
A real number is distinguished from an imaginary or complex number. It is what we call any rational or irrational number. It is a number we expect to find on the number line. It is a number we need for measuring.
The real numbers are the subject of calculus and of scientific measurement.
A real variable is a variable that takes on real values.
Problem 12. Let x be a real variable, and let 3 < x < 4. Name five values that x might have.
For example, 3.1, 3.14, 
, 
, 
.
Problem 13. If the square root is to be a real number, then the radicand may not be negative. (There is no such real number, for example, as 
.)
If is to be real, then we must have x ≥ 0.
(If you are not viewing this page with Internet Explorer 6 or Firefox 3, then your browser may not be able to display the symbol ≥, "is greater than or equal to"; or ≤, "is less than or equal to.")
Therefore, what values are permitted to the real variable x ?
a) 
x − 3 ≥ 0; that is, x ≥ 3.
b) 
1 + x ≥ 0; x ≥ −1.
c) 
1 − x ≥ 0; −x ≥ −1, which implies x ≤ 1.
d) 
x² ≥ 0. In this case, x may be any real number.
Next Lesson: Simplifying radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2012 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com