21
LOGARITHMIC AND EXPONENTIAL FUNCTIONS
Exponential and logarithmic equations
Writing a sum as one logarithm
THE LOGARITHMIC FUNCTION WITH BASE b is the function
y = logb x.
b is normally a number greater than 1 (although it need only be greater than 0 and not equal to 1). The function is defined for all x > 0. Here is its graph for any base b.
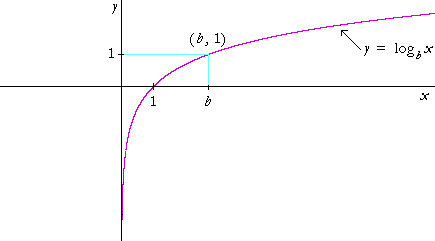
Note the following:
• For any base, the x-intercept is 1. Why?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
The logarithm of 1 is 0. y = logb1 = 0.
• The graph passes through the point (b, 1). Why?
The logarithm of the base is 1. logbb = 1.
• The graph is below the x-axis—the logarithm is negative—for
0 < x < 1.
Which numbers are those that have negative logarithms?
Proper fractions.
• The function is defined only for positive values of x.
logb(−4), for example, makes no sense. Since b is always positive,
no power of b can produce a negative number.
• The range of the function is all real numbers.
• The negative y-axis is a vertical asymptote.
Example 1. Translation. Here is the graph of the natural logarithm,
y = ln x.
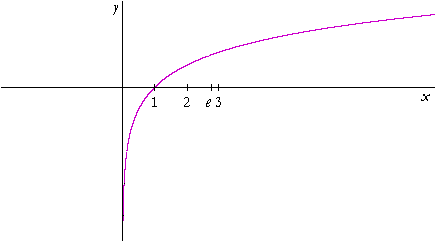
And here is the graph of y = ln (x − 2)—which is its translation 2 units to the right.
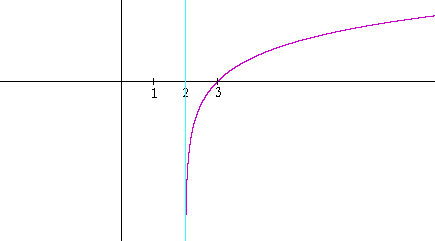
The x-intercept has moved from 1 to 3. And the vertical asymptote has moved from x = 0 to x = 2.
Problem 1. Sketch the graph of y = ln (x + 3).
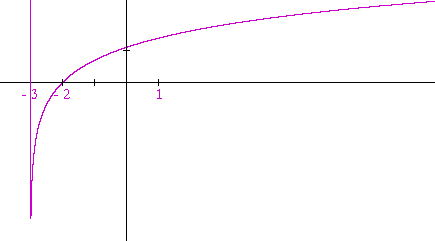
This is a translation 3 units to the left. The x-intercept has moved from 1 to −2. And the vertical asymptote has moved from x = 0 to x = −3.
Exponential functions
By definition:
logby = x means bx = y.
Corresponding to every logarithm function with base b, we see that there is an exponential function with base b:
y = bx.
The argument of an exponential function is the exponent.
An exponential function is defined for every real number x. Here is its graph for any base b:
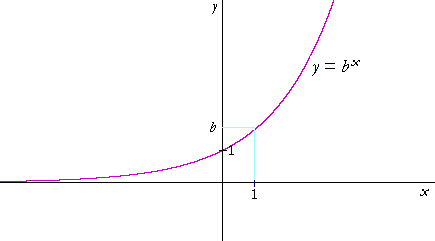
There are two important things to note:
• The y-intercept is at (0, 1). b0 = 1.
• The negative x-axis is a horizontal asymptote. For when x is a large negative number—e.g. b−10,000—then y is a very small positive number.
Problem 2.
a) Let f(x) = ex. Write the function f(−x).
f(−x) = e−x
The argument x is replaced by −x.
b) What is the relationship between the graph of y = ex and the graph
b) of y = e−x ?
y = e−x is the reflection about the y-axis of y = ex.
c) Sketch the graph of y = e−x.
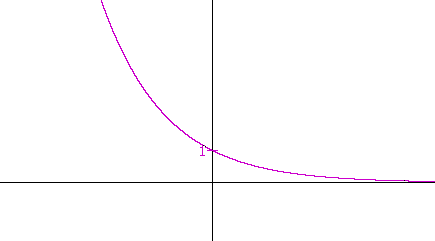
Inverse relations
The exponential function and logarithmic function with base b are inverses.
f(x) = logbx and g(x) = bx are inverses.
They satisfy the definition.
f(g(x)) = f(bx) = logbbx = x.
We saw that in the previous Topic.
And:
g(f(x)) = g(logbx) = blogbx) = x.
That embodies the definition of a logarithm: logbx is the exponent to which b must be raised to produce x.
Problem 3. Evaluate the following.
| a) log225 | = 5 | b) log552x | = 2x | c) log 106.2 | = 6.2 | ||
| d) 2log25 | = 5 | e) 5log5(x − 1) | = x − 1 | f) 10log 100 | = 100 | ||
Problem 4.
a) What function is the inverse of y = ln x?
y = ex.
b) Let f(x) = ln x and g(x) = ex, and show that f and g satisfy the
b) inverse relations.
f(g(x)) = ln ex = x,
g(f(x)) = eln x = x.
Here are the graphs of y = ex and y = ln x :
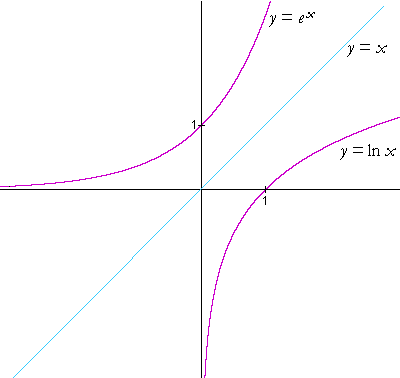
As with all pairs of inverse functions, their graphs are symmetrical with respect to the line y = x. (See Topic 19.)
Problem 5. Evaluate the following.
| a) ln ex + 1 | = x + 1 | b) eln (x − 5) | = x − 5 |
Problem 6. Evaluate ln earccos (−1).
ln earccos (−1) = arccos (−1) = π.
"The angle whose cosine is −1 is π."
Topic 19 of Trigonometry.
Exponential and logarithmic equations
Example 2. Solve this equation for x :
5x + 1 = 625.
Solution. When the unknown x appears as an exponent, then to extract it, take the inverse function of both sides.
In this example, take the logarithm with base 5 of both sides.
| log55x + 1 | = | log5625 | |
| x + 1 | = | log5625 | |
| x + 1 | = | 4 | |
| x | = | 3. | |
In general, if we have an equation,
| f(x) | = | a, | |
| then for any argument x, if g is the inverse of f: | |||
| x | = | g(a). | |
Example 3. Solve for x :
2x − 4 = 3x
Solution. We may take the log of both sides either with the base 2 or the base 3. Let us use base 2:
| log22x − 4 | = | log23x | |
| x − 4 | = | log23x | |
| x − 4 | = | x log23, according to the 3rd Law | |
| x − x log23 | = | 4 | |
| x(1 − log23) | = | 4 | |
| x | = | 4 1 − log23 |
|
log23 is some number. The equation is solved.
Problem 7. Solve for x :
| 2x − 5 | = | 32. | |
| log22x − 5 | = | log232 | |
| x − 5 | = | 5 | |
| x | = | 10 | |
Problem 8. Solve for x. The solution may be expressed as a logarithm.
103x − 1 = 22x + 1
| log 103x − 1 | = | log 22x + 1 | |
| 3x − 1 | = | (2x + 1) log 2 | |
| 3x − 1 | = | 2x log 2 + log 2 | |
| 3x − 2x log 2 | = | 1 + log 2 | |
| x(3 − 2 log 2) | = | 1 + log 2 | |
| x | = | 1 + log 2 3 − 2 log 2 |
|
Problem 9. Solve for x :
| esin x | = | 1 | |
| ln esin x | = | ln 1 | |
| sin x | = | 0 | |
| x is the radian angle whose sine is 0: | |||
| x | = | nπ. | |
Problem 10. Solve for x :
| log4(3x − 5) | = | 0. |
| If we let each side be the exponent with base 4, then | ||
| 3x − 5 | = | 40 = 1 |
| 3x | = | 6 |
| x | = | 2. |
Problem 11. Solve for x :
| log2(x2 + 7) | = | 4. |
| x2 + 7 | = | 24 = 16 |
| x2 | = | 16 − 7 = 9 |
| x | = | ±3. |
Writing a sum as one logarithm
Example 4. Use the laws of logarithms to write the following as one logarithm.
log x + log y − 2 log z.
| Solution. log x + log y − 2 log z | = | log | xy − log z2 |
| = | log | xy z2 |
|
Problem 12. Write as one logarithm:
k log x + m log y − n log z
![]()
Problem 13. Write as one logarithm:
log (2x − 8) − log (x2 − 16).
| log (2x − 8) − log (x2 − 16) | = | log | 2x − 8 x2 − 16 |
| = | log | 2(x − 4) (x − 4)(x + 4) |
|
| = | log | 2 x + 4 |
|
Example 5. By means of this identity—
n = logbbn
—we can write any number n as a logarithm in any base b.
For example,
| 7 | = | log227 |
| 5.9 | = | log335.9 |
| t | = | ln et |
| 3 | = | log 1000 |
Problem 14.
| a) | 2 = ln e2 | b) | 1 = ln e |
Example 6. Write the following sum as one logarithm:
logbx + n.
| Solution. | logbx + n | = | logbx + logbbn |
| = | logbxbn. | ||
Problem 15. Write these two terms as one logarithm:
log 2 + 3.
| log 2 + 3 | = | log 2 + log 103 |
| = | log 2 × 103 | |
| = | log 2000. | |
Problem 16. Write as one logarithm:
ln A − t.
| ln A − t | = | ln A − ln et |
| = | ln A + ln e−t | |
| = | ln Ae−t | |
Example 7. Solve for x:
log (2x + 1) = log 11.
Solution. If we let each side be the exponent with base 10, then
| 2x + 1 | = | 11. |
| That implies | ||
| x | = | 5. |
We may conclude, then, that if an equation looks like this:
| logb A | = | logb B, | |
| then | |||
| A | = | B. |
Problem 17. Solve for x:
| log2x + log2(x + 2) | = | 3. |
| log2[x(x + 2)] | = | log223 |
| x(x + 2) | = | 23 = 8. |
| x2 + 2x − 8 | = | 0 |
| (x − 2)(x + 4) | = | 0 |
| x | = | 2 or −4. |
We must reject the solution x = − 4, however, because the negative number −4 is not in the domain of log2x.
Problem 18. Solve for x.
| ln (1 + x) − ln (1 − x) | = | 1. |
| = | ln e. | |
| = | e | |
| 1 + x | = | e − ex |
| ex + x | = | e − 1 |
| (e + 1)x | = | e − 1 |
| x | = | |
This Topic concludes our study of functions and their graphs.
Next Topic: Sigma notation for sums
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
