14
MULTIPLE ROOTS
POINT OF INFLECTION
WHEN WE STUDIED quadratic equations, we saw what it means for a polynomial to have a double root. We now want to learn about the graphs of polynomials that have multiple roots.
For example, this polynomial
y = (x − 1)3 = (x − 1)(x − 1)(x − 1)
has a triple root: 1, 1, 1.
1. a) What does it mean for a polynomial to have a root
1. a) (or zero) of multiplicity k > 1?
1. The same root is repeated k times.
1. b) Algebraically, how can we recognize that r is a root of
1. a) multiplicity k?
1. x − r is a factor k times; i.e., (x − r)k is a factor.
For example, in this polynomial,
(x − 3)4(x + 1)5
3 is a root of multiplicity 4, and −1 is a root of multiplicity 5.
2. Which of these
graphs is concave upward and which is
2. concave downward?
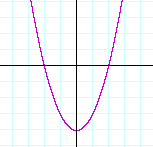
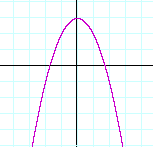
The graph on the left is concave upward. The other is concave downward.
Imagine an arrow within each graph with its nock (its foot) at the turning point. Then in the graph on the left, the arrow will point up: concave upward; in the graph on the right, it will point down: concave downward.
3. What is a point of inflection?
The value of x where a graph changes concavity; from concave upward to concave downward, or vice-versa.
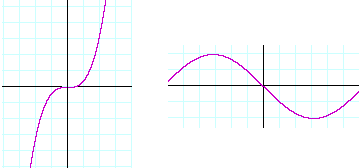
In each of these graphs, x = 0 is a point of inflection. At x = 0 -- at the origin -- each graph changes from concave downward to concave upward.
As the calculus student will learn, at a point of inflection the second derivative is 0.
4. a) What happens to the graph at a root of even multiplicity?
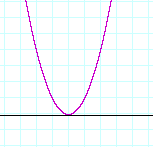
4. The graph touches the x-axis (is tangent to it), but does
4. not cross it.
4. b) What happens to the graph at a root of odd multiplicity?
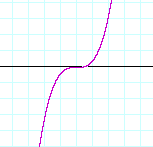
4. The graph crosses the x-axis, and it is a point of inflection.
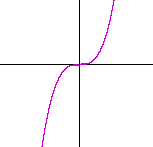
Problem 1. Name all the roots, and sketch the graph, of y = x3.
The roots are 0, 0, 0. Here is the graph.
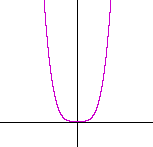
Problem 2. Name all the roots, and sketch the graph, of y = x4.
The roots are 0, 0, 0, 0. Here is the graph.
Example. Name the roots of this polynomial. What is its degree? Sketch its graph.
y = (x + 2)2(x − 1)3
Answer. −2 is a root of multiplicity 2, and 1 is a root of multiplicity 3. These are the 5 roots:
−2, −2, 1, 1, 1.
This polynomial is of the 5th degree, which is odd. Therefore, the graph begins on the left below the x-axis.
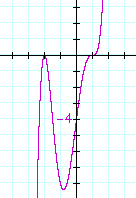
−2 is a root of even multiplicity -- at −2 the graph is tangent to the x-axis. 1 is a root of odd multiplicity. 1 is a point of inflection.
Problem 3. Name the roots of this polynomial. What is its degree? Sketch its graph.
y = x3(x + 2)4(x − 3)5
This polynomial is of degree 3 + 4 + 5 = 12. These are the 12 roots:
0, 0, 0, −2, −2, −2, −2, 3, 3, 3, 3, 3.
Here is the graph.
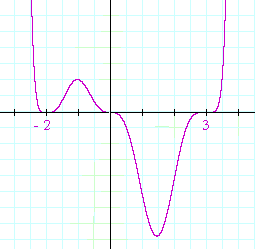
This polynomial is of even degree, therefore the graph begins on the left above the x-axis. −2 is a root of even multiplicity, therefore at −2, the graph is tangent to the x-axis.
0 is a root of odd multiplicity, therefore 0 is a point of inflection.
3 is a root of odd multiplicity, therefore 3 is also a point of inflection.
Next Topic: Reflections and symmetry
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
