10
QUADRATICS
Polynomials of the 2nd degree
Solving the quadratic equation by factoring
The sum and product of the roots
QUADRATIC IS ANOTHER NAME for a polynomial of the 2nd degree. 2 is the highest exponent.
1. A polynomial function of the 2nd degree has what form?
y = ax2 + bx + c
2. A quadratic equation has what form?
ax2 + bx + c = 0
3. What do we mean by a root of a quadratic?
A solution to the quadratic equation.
4. A quadratic always has how many roots?
Two, real or complex.
5. The graph of a quadratic is always the form called -- ?
A parabola.
6. What are the three methods for solving a quadratic equation,
6. that is, for finding the roots?
1. Factoring. 2. Completing the square.
3. The quadratic formula.
We begin with the method of factoring. In the next Topic, we will present both Completing the square and The quadratic formula.
7. If a product of factors is 0 -- if ab = 0 -- then what can you
7. conclude about the factors a, b ?
Either a = 0, or b = 0.
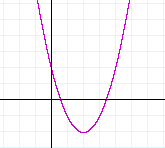
Example 1. Solution by factoring.
f(x) = x2 −2x −3. Find the roots of f(x), and sketch the graph of y = f(x).
Solution. x2 −2x −3 = (x + 1)(x − 3).
Therefore, the roots are −1 and 3. (See Lesson 37 of Algebra.) They are the x-intercepts of the graph.
The y-intercept is the constant term, −3.
In every polynomial, the y-intercept is the constant term because the constant term is the value of y when x = 0.
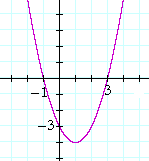
Example 2. A double root
f(x) = x2 −10x + 25. Find the roots of
f(x), and sketch the graph of y = f(x).
Solution. x2 −10x + 25 =
(x − 5)(x − 5) = (x − 5)2. The two roots are equal, they are 5, 5. 5 is called a double root. (See Lesson 37 of Algebra, Question 4.)
At a double root, the graph does not cross the x-axis. It just touches it.
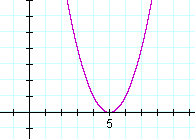
A double root occurs when the quadratic is a perfect square trinomial: x2 ±2ax + a2; that is, when the quadratic is the square of a binomial: (x ± a)2.
Example 3. How many real roots, i.e. roots that are real numbers, has the quadratic of each graph?
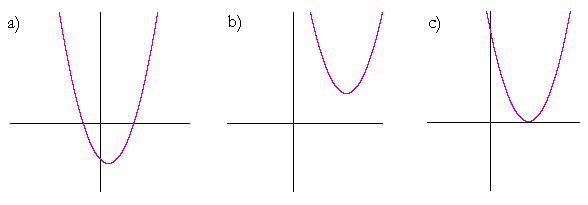
Answer. Graph a) has two real roots. It has two x-intercepts.
Graph b) has no real roots. It has no x-intercepts. Both roots are complex.
Graph c) has two real roots. But they are a double root.
Example 4. Quadratic inequality.
Solve this inequality:
x2 − 4x − 5 < 0.
To do it, inspect the graph of
y = x2 − 4x − 5.
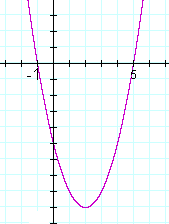
Solution. For which values of x will that quadratic be negative? That is, where is the graph below the x-axis?
The graph is negative between the roots, which are −1 and 5. The solution to the inequality is −1 < x < 5.
We can also observe that the quadratic will have positive values -- the graph will be above the x-axis -- to the left and right of the roots:
x < −1 or x > 5.
While the quadratic will have the value 0 at the roots.
We have now covered the three possibilities:
That quadratic is equal to 0 at the two roots.
It is less than 0 between the two roots.
It is greater than 0 to the left and right of the two roots.
These three possiblities, which are true for any real number, has the fancy name of the Law of Trichotomy. Any number must be either equal to, less than, or greater than 0.
The Law of Trichotomy also takes this form:
For any real numbers a, b, either a = b, a < b, or a > b.
We must be able to know, though, which of those possibilities is true. For any two numbers, we must be able to know their relative order. That is inherent in the meaning of a "number."
Problem 1. Sketch the graph of y = x2 − 2x −8. That is, show the x- and y-intercepts.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
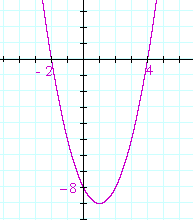
x2 −2x − 8 = (x + 2)(x − 4). Therefore, the roots are −2, 4. The y-intercept is the constant term, −8.
Problem 2. Sketch the graph of
y = x2 + 4x + 4.
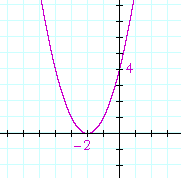
x2 + 4x + 4 = (x + 2)2. There is a double root at −2. The y-intercept is the constant term, 4.
Problem 3.
a) To solve this quadratic inequality—
x2 + 2x − 3 > 0
—inspect the graph of
y = x2 + 2x − 3.
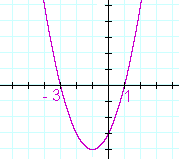
The quadratic will be positive -- above the x-axis -- for values of x to the left and right of the roots. The solution is
x < −3 or x > 1.
b) Solve this quadratic inequality:
x2 + 2x − 3 < 0.
−3 < x < 1.
The quadratic will be negative between the roots.
Problem 4. A quadratic has the following roots. Write each quadratic as a product of linear factors.
a) 3, 4 (x − 3)(x − 4)
b) −3, −4 (x + 3)(x + 4)
c) −r, s (x + r)(x − s)
d) 3 + ![]() , 3 −
, 3 − ![]() (x − 3 −
(x − 3 − ![]() )(x −3 +
)(x −3 + ![]() )
)
The sum and product of the roots
Theorem. In a quadratic whose leading coefficient is 1:
The sum of the roots is the negative of the coefficient of x;
the product of the roots is the constant term.
That is, if
x2 + bx + c = 0,
and the roots are r and s, then
| r + s | = | −b, |
| rs | = | c. |
For if the roots are r and s, then the quadratic is
| (x − r)(x − s) | = | x2 − rx − sx + rs |
| = | x2 − (r + s)x + rs. | |
The coefficient of x is −(r + s), which is the negative of the sum of the roots. The constant term is rs, which is their product.
Example 5. Construct the quadratic whose roots are 2 and 3.
Solution. The sum of the roots is 5, their product is 6, therefore the quadratic is x2 − 5x + 6.
The sum of the roots is the negative of the coefficient of x. The product of the roots is the constant term.
Example 6. Construct the quadratic whose roots are 2 + ![]() , 2 −
, 2 − ![]() .
.
Solution. The sum of the roots is 4. Their product is the Difference of two squares: 22 − (![]() )2 = 4 − 3 = 1.
)2 = 4 − 3 = 1.
The quadratic therefore is x2 − 4x + 1.
Example 7. Construct the quadratic whose roots are 2 + 3i, 2 − 3i, where i is the complex unit.
Solution. The sum of the roots is 4. The product again is the Difference of Two Squares: 4 − 9i2 = 4 + 9 = 13.
The quadratic with those roots is
x2 − 4x + 13.
Problem 5. Construct the quadratic whose roots are −3, 4.
The sum of the roots is 1. Their product is −12. Therefore, the quadratic is x2 − x − 12.
Problem 6. Construct the quadratic whose roots are 3 + ![]() , 3 −
, 3 − ![]() .
.
The sum of the roots is 6. Their product is 9 − 3 = 6.
Therefore, the quadratic is x2 − 6x + 6.
Problem 7. Construct the quadratic whose roots are 2 + i![]() , 2 − i
, 2 − i![]() .
.
The sum of the roots is 4. Their product is 4 − (i![]() )2 = 4 + 5 = 9.
)2 = 4 + 5 = 9.
Therefore, the quadratic is x2 − 4x + 9.
*
More generally, for any coefficient of x2, that is, if the quadratic is
ax2 + bx + c,
and the roots are r and s, then
| r + s | = | − | b a |
, |
| rs | = | c a |
. | |
When a = 1, we have the theorem above.
Next Topic: Completing the square
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
