11
COMPLETING THE SQUARE
IF WE TRY TO SOLVE this quadratic equation by factoring
x2 + 6x + 2 = 0
we cannot. Therefore, we use a method called completing the square. That means to make the quadratic into a perfect square trinomial, i.e. the form
a2 + 2ab + b2 = (a + b)2.
This method is valid only when 1 is the coefficient of x2.
1) Transpose the constant term to the right:
x2 + 6x = −2
2) Add a square number to both sides: Add the square of half the coefficient of x. In this case, add the square of 3:
x2 + 6x + 9 = −2 + 9
The left-hand side is now the perfect square of (x + 3).
(x + 3)2 = 7.
That equation has the form
| a2 | = | b, | |
| which implies | |||
| a | = | ± |
|
| Therefore, | |||
| x + 3 | = | ± |
|
| x | = | −3 ± |
|
The solutions to
x2 + 6x + 2 = 0
are the conjugate pair,
−3 + ![]() , −3 −
, −3 − ![]() .
.
We can check this. The sum of those roots is −6, which is the negative of the coefficient of x. And the product of the roots is
(−3)2 − (![]() )2 = 9 − 7 = 2,
)2 = 9 − 7 = 2,
which is the constant term. Thus both conditions on the roots are satisfied. Those are the two roots of the quadratic.
Problem. Solve this quadratic equation by completing the square.
x2 − 2x − 2 = 0
To see the solution, pass your mouse over the colored area.
To cover the solution again, click "Refresh" ("Reload").
| x2 − 2x | = | 2 |
| x2 − 2x + 1 | = | 2 + 1 |
| (x − 1)2 | = | 3 |
| x − 1 | = | ± |
| x | = | 1 ± |
See Lesson 37 of Algebra, Problems 6 and 7.
Before considering the quadratic formula, note that half of any
| number b is | b 2 |
. Half of 5 is | 5 2 |
. Half of | p q |
is | p 2q |
. | ||||
(Lesson 27 of Arithmetic, Question 4.)
The quadratic formula
Theorem. If
ax2 + bx + c = 0,
Theorem. then
![]()
To prove this, we will complete the square. But to do that, the coefficient of x2 must be 1. Therefore, we will divide both sides of the original equation by a:
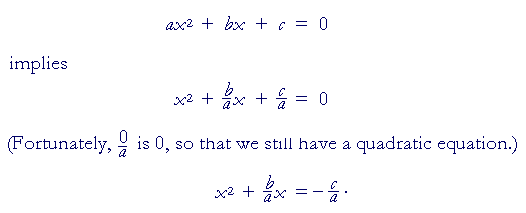
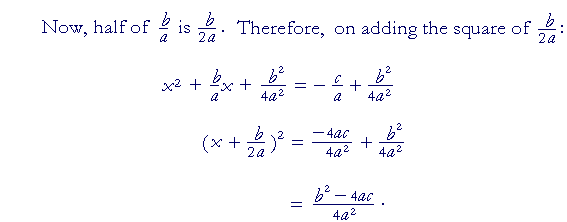
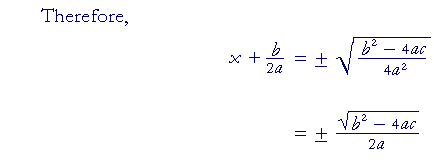
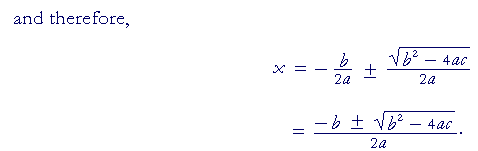
This is the quadratic formula.
Next Topic: Synthetic division by x − a
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
