Lesson 11
THE MEANING OF DIVISION
In this Lesson, we will address the following:
- What is the problem of "division"?
- If we divide a number into equal parts, how can we know how many there are in each part?
- What is a rate?
- Which numbers will be exactly divisible by a given number? Exact versus inexact division.
Section 2. Decomposing the dividend
IN MULTIPLICATION we are given two numbers --
4 × 15 = ?
-- the multiplier and the multiplicand, and we have to name their product.
But in what is called the inverse of multiplication, we are given the product and the multiplicand --
? × 15 = 60
-- and we have to name the multiplier.
"What number times 15 equals 60?"
That is,
"How many times do we have to add 15 to get 60?"
We call that division because 60 is being divided by -- cut into equal parts -- by 15.
We write:
60 ÷ 15 = 4.
"60 divided by 15 equals 4."
That is true because
4 × 15 = 60.
"4 times 15 equals 60."
Equivalently, we could subtract 15 from 60 four times. Multiplication is repeated addition. Therefore we can think of division as repeated subtraction.
When we write:
60 ÷ 15 = 4,
then 15, the number on the right of the division sign ÷ , is called the divisor. It is the number we have to multiply to get 60.
60 is called the dividend; it is the number being divided by 15.
4 is called the quotient. It is the number of times we must multiply 15 to get 60. In the figure, the quotient is the number of equal parts into which the dividend has been divided.
| 1. | What is the problem of "division"? | ||
| Dividend ÷ Divisor | = | Quotient. | |
| Quotient × Divisor | = | Dividend. | |
| We are to name the number of times one number, called the Divisor, is contained in another number, called the Dividend. That number of times is called the Quotient. |
|||
| Equivalently, we are to say what number times the Divisor will equal the Dividend. That is, how many times do we have to add the Divisor so that it will equal the Dividend? | |||
| Or, how many times we could subtract the Divisor from the Dividend? | |||
A divisor may not be 0 -- 6 ÷ 0 -- because any number
times 0 will still be 0. Division by 0 is an excluded operation.
As for 0 ÷ 0, that is ambiguous because it could be any number. Any number times the divisor 0 will equal the dividend 0.
Example 1. This figure shows how the numbers 1, 2, 3, 4, and 6 go into -- are contained in -- 12.

6 goes into 12 two times. 12 ÷ 6 = 2.
4 goes into 12 three times. 12 ÷ 4 = 3.
3 goes into 12 four times. 12 ÷ 3 = 4.
2 goes into 12 six times. 12 ÷ 2 = 6.
1 goes into 12 twelve times. 12 ÷ 1 = 12.
Example 2. A bottle of juice contains 18 ounces. How many times could you fill a 6 ounce glass?
Answer. Any problem that asks "How many times?" is a division problem. So the question is: How many times is 6 ounces contained in 18?
18 ÷ 6 = 3.
"18 divided by 6 equals 3."
You could fill the glass 3 times.
Here is the picture of 18 ÷ 6 :
![]()
6 goes into 18 three times. That is,
3 × 6 = 18.
Equivalently, we could subtract 6 from 18 three times.
Here, on the other hand, is the picture of 18 ÷ 3:
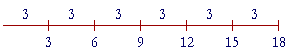
18 can be divided into six 3's.
18 ÷ 3 = 6.
"3 goes into 18 six times."
6 × 3 = 18.
| Dividend ÷ Divisor | = | Quotient |
| Quotient × Divisor | = | Dividend |
For such a simple problem the student should not write the division box.
![]()
It is not necessary to prepare for long division in the way they had to 100 years ago.
See Example 11, and Lesson 12.
Example 3. What number times 10 will equal 72?
Answer. Again, this is a division problem. The number that follows the word "times" is the divisor. We have to divide 72 by 10.
On separating one decimal digit:
72 ÷ 10 = 7.2
That is,
7.2 × 10 = 72.
Example 4. If it takes 3 yards of material to make a suit, how many suits could be made from a piece of material that is 15 yards?
Answer. We have to cut 3 yards from 15 yards as many times as we can. That number of times is 15 ÷ 3.

15 ÷ 3 = 5.
That is,
15 yd ÷ 3 yd = 5,
because
5 × 3 yd = 15 yd.
You could make 5 suits.
This problem illustrates the following: The dividend and divisor must be units of the same kind. We can only divide yards by yards, dollars by dollars, hours by hours. We cannot divide 8 apples by 2 oranges --
8 apples ÷ 2 oranges = ?
-- because there is no number times 2 oranges that will equal 8 apples![]()
What is more, we see that the quotient is always a pure number.
Dividend ÷ Divisor = Quotient.
It is the number that multiplies the divisor to produce the dividend.
Example 5. A bus is scheduled to arrive every 12 minutes. In the course of 2 hours, how many buses will arrive?
Answer. How many times is 12 minutes contained in 2 hours? But the units must be the same. Since 1 hour = 60 minutes, then 2 hours = 2 × 60 = 120 minutes.
Therefore,
120 minutes ÷ 12 minutes = 10.
10 times 12 minutes = 120 minutes. (Lesson 4.)
In the course of 2 hours, 10 buses will arrive.
(See Problem 6 at the end of the Lesson.)
Division into equal parts
| 2. | If we divide a number into equal parts, how can we know how many there are in each part? |
| Divide by the number of equal parts. | |
If we divide into 2 equal parts,
![]()
then to know how many there are in each part, divide by 2.
If we divide into 3 equal parts,
![]()
divide by 3. And so on.
That is why to divide the whole of something, which is 100%, into 100 equal parts -- that is, to find 1% of a number -- we divide by 100. (Lesson 4, Question 6.)
Example 6. If we divide 28 people into four equal parts, then how many will be in each part?
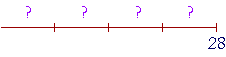
In Lesson 15 we will see that we are taking a "quarter" or a "fourth" of 28 people.
Solution. Divide by 4. 28 ÷ 4 = 7.
There will be 7 people in each part.
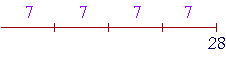
But that is the picture of 28 ÷ 7. Why does 28 ÷ 4 give the right answer?
Because of the order property of multiplication. 28 ÷ 4 = 7 means
7 × 4 = 28.
But that implies
4 × 7 = 28.
That means 28 is made up of four 7's.
Example 7. Christopher bought 3 shirts for a total of $66. Each one cost the same. How much did each one cost?
Solution. If we divide $66 into 3 equal parts, we will know the answer.
66 ÷ 3 = ?
What number times 3 will be 66?
Equivalently, 3 times what number will be 66?
3 × 22 = 66.
Each shirt cost $22.
In Lesson 15, we will speak simply of taking a third of $66, and the question of division never comes up.
A problem in which we relate units of different kinds -- dollars per shirt, for example -- is called a rate problem, as we are about to see.
| 3. | What is a rate? |
| A rate is a relationship between units of different kinds. Miles per hour. Dollars per person. And so on. | |
A rate is typically indicated by per, which means for each or in each.
In a calculation, per always indicates division.
Example 8. In a certain country, the unit of currency is the corona. With $11 Ana was able to buy 55 coronas. What was the rate of exchange? That is, how many coronas per dollar?
Solution. Follow the sequence: coronas per dollar: 55 ÷ 11 = 5.
The rate of exchange was 5 coronas per dollar.
Again, a rate problem involves dividing a number into equal parts. In this example, we divided 55 coronas into 5 equal parts of 11 coronas each.
5 × 11 coronas = 55 coronas.
But that implies 11 × 5 coronas = 55 coronas:
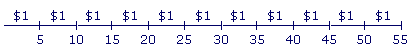
Each group of 5 was worth $1. That was the rate of exchange. 5 coronas per dollar.
To preserve the meanings of multiplication and division, we must relate units of the same kind, even though that is not how it might appear.
Exact versus inexact division
| 4. | Which numbers will be exactly divisible by a given number? |
| The multiples of that number. | |
The numbers exactly divisible by 3 are the multiples of 3:
3, 6, 9, 12, and so on.
And since they are divisible by 3, so are
30, 60, 90, 120, . . .
300, 600, 900, 1200, . . .
Since those are the multiples of 3, we say that 3 is their divisor. In other words, we say that one number is a divisor of a second if the second is its multiple.
A number will go evenly into every one of its multiples.
The numbers exactly divisible by 8 are the multiples of 8:
8, 16, 24, 32, . . .
80, 160, 240, 320, . . .
800, 1600, 2400, 3200, . . .
Example 9. A bottle holds 35 ounces. A glass holds 8 ounces. How many glasses can you fill from that bottle?
Solution. We must calculate 35 ÷ 8. Now, 8 goes into 32 exactly, but 8 does not go into 35 exactly:
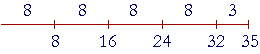
There is a remainder of 3.
35 = 4 × 8 + 3.
Therefore you could fill 4 glasses, and 3 ounces will remain in the bottle.
We write the following:
35 ÷ 8 = 4 R 3
The remainder 3 is what we have to add to 4 × 8 to get 35.
Possible remainders
Say there are a large number of people, and we want to divide them into groups of 5.
![]()
But say we discover that there is not an exact number of 5's. Then how many people might we not be able to group? How many people might remain?
Answer: Either 1, or 2, or 3, or 4. Because if more than 4 remained, we could make another group of 5![]()
The point is:
The remainder is always less than the divisor.
If we divide by 5, then the possible remainders are 1, 2, 3, or 4.
Example 10.
a) If 7 is the divisor, what are the possible remainders?
Answer. 1, 2, 3, 4, 5, 6.
b) How many 7's are there in 61?
Answer. 8. 8 × 7 is 56 -- plus 5 is 61.
61 ÷ 7 = 8 R 5.
That is,
61 = 8 × 7 + 5.
The remainder 5 is what we must add to 56 to get 61.
Example 11. Prove: 47 ÷ 9 = 5 R 2.
Proof. 5 × 9 + 2 = 45 + 2 = 47.
Example 12. 53 ÷ 8.
Say the whole number quotient and the remainder. Do not write the division box.
Say:
"8 goes into 53 six times -- 48 -- with 5 left over."
53 ÷ 8 = 6 R 5.
The remainder is the number you have to add to 48 to get 53.
How would you know that you have to add 5? 48 plus what number ends in 3? 8 plus 5 ends in 3. (13.) 5 is the remainder.
Or:
48 plus 2 is 50, plus 3 is 53.
48 + 5 = 53.
Example 13. 31 ÷ 4.
"4 goes into 31 seven times -- 28 -- with 3 left over."
See Problems 7 - 11.
The division bar
In what follows, we will signify division in this way:
| 16 8 |
= 2 |
"16 divided by 8 is 2."
| Dividend Divisor |
= Quotient |
The check is:
Quotient × Divisor = Dividend
The horizontal line separating 16 and 8 is called the division bar. The division bar is also used to signify a fraction, because a fraction sometimes requires division of the numerator by the denominator. (Lessons 20 and 24.) We also use the division bar to indicate the ratio of two numbers. (Lesson 20.)
| Example 14. | 280 7 |
= ? |
"280 divided by 7 is what number?"
Answer. Ignore the 0. 7 goes into 28 four (4) times. Therefore 7 goes into 280 forty (40) times.
| 280 7 |
= 40. |
40 times 7 is 280.
In other words, since 28 is divisible by 7, then so is '28' followed by any number of 0's.
280 2800 28,000 280,000 . . .
| Example 15. | 5400 9 |
= | ? |
Answer. 600. Because 600 × 9 = 5400.
| Example 16. | $246 100 |
= | $2.46 |
This is $246 ÷ 100. It is 1% of $246. (Lesson 4.)
| Example 17. 5 ÷ 8 = | 5 8 |
| 5 ÷ 8 is simply the fraction | 5 8 |
-- which, because of the division bar, |
we can interpret as 5 ÷ 8
In the next Lesson we will see how to express 5 ÷ 8 as a decimal.
Please "turn" the page and do some Problems.
or
Section 2. Mental calculation: Decomposing the dividend
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
