Lesson 9 Section 2
Decomposing the multiplicand:
The distributive property of multiplication
In Section 1 we saw how to decompose the multiplier.
12 × 7 = 10 × 7 + 2 × 7.
We will now see how to decompose the multiplicand.
2 × 105 = 2 × 100 + 2 × 5.
When we decompose 105 into 100 + 5, we can then "distribute" 2 to 100 and to 5.
| 4. | What is the distributive property of multiplication? |
| When multiplying a sum or a difference, we may multiply each term of the sum or difference, and then add or subtract the partial products. | |
| 2 × (100 + 5) | = | 2 × 100 + 2 × 5 |
| = | 200 + 10 | |
| = | 210. | |
| 2 × (100 − 5) | = | 2 × 100 − 2 × 5 |
| = | 200 − 10 | |
| = | 190. | |
In each case, we "distributed" 2 to both 100 and 5.
We cannot emphasize enough the importance of the distributive property. It is the basis not only of mental calculation, as we are about to see, but it is the basis of the traditional written method as well. Moreover, it is a theorem that we can prove.
| 5. | How can we apply the distributive property to mental calculation? |
 |
|
| Decompose or expand the multiplicand mentally into its units. Distribute the multipier from left to right to each unit, then add the partial products. | |
| Example 1. 3 × 24 | = | 3 × 20 + 3 × 4 |
| = | 60 + 12 | |
| = | 72. | |
We expanded 24 into 20 + 4, and then "distributed" 3 to each one.
Look:
| 3 × 24 | = | 24 + 24 + 24 |
| = | 20 + 4 + 20 + 4 + 20 + 4 | |
| = | 20 + 20 + 20 + 4 + 4 + 4 | |
| = | 3 × 20 + 3 × 4. | |
The repeated addition of 24 is equal to the repeated addition of 20, plus the repeated addition of 4.
(For a general proof, see Appendix 4.)
Example 2. Multiply 5 × 37 mentally.
Technique. Distribute 5 to 30 + 7. Say:
"150 plus 35 is 185."
Multiply the numbers as you read them, from left to right. The last number you say is the answer.
Example 3. Multiply mentally 8 × 46.
"320 + 48 = 368."
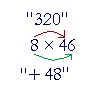
Example 4. 800 × 460
Ignore the final 0's and multiply 8 × 46. But we just saw that
8 × 46 = 368.
Therefore:
800 × 460 = 368,000.
This is "368" with three 0's.
Example 5. Multiply 6 × 7.30. (Treat problems with decimal points as dollars and cents.)
Technique. Expand 7.30 mentally into 7 + .30 Then
| 6 × 7.30 | = | 42 + 1.80 | (Lesson 9) |
| = | 43.80. | ||
Example 6. What is the price of five items that cost $3.25 each?
Answer. Since 4 × $.25 = $1.00, then 5 × $.25 = $1.25. Say,
"5 × 3.25 = 15 + 1.25 = 16.25"
Example 7. Multiply 2 × 438 mentally.
| Solution. | 2 × 438 | = | 800 + 60 + 16 |
| = | 876. | ||
The point is to say each partial sum. Look at 2 × 438 and say,
"860 + 16 is 876."
(Again, in 438, the 4 signifies 400, and the 3 signifies 30. Lesson 2.)
Example 8. Multiply 4 × 709.
| Solution. | 4 × 709 | = | 4 × 700 + 4 × 0 + 4 × 9 |
| = | 2800 + 0 + 36 | ||
| = | 2836. | ||
Note: Any number times 0, or 0 times any number, is 0.
Therefore, to calculate 4 × 709, simply ignore the 0 and say:
"2800 + 36 is 2836."
Example 9. Multiply 8,000 × 4,310.
Technique. Ignore the final 0's:
| 8 × 431 | = | 3200 + 240 + 8 |
| = | 3440 + 8 | |
| = | 3448. | |
Now replace the four 0's:
8,000 × 4,310 = 34,480,000
Example 10. How much is 20% of $68?
Solution. 10% of $68 is $6.80. (Lesson 4.) Therefore, 20% is
2 × $6.80 = $12 + $1.60 = $13.60.
Example 11. How many hours are there in one week? How many minutes are there?
Solution. There are 24 hours in one day, and there are 7 days in a week. Therefore,
7 × 24 = 140 + 28 = 168 hours.
Now, in each hour there are 60 minutes. To multiply
60 × 168,
ignore the 0 and multiply
| 6 × 168 | = | 600 + 360 + 48 |
| = | 960 + 48 | |
| = | 1008. | |
Now replace the 0 we ignored:
10080.
In one week, then, there are 10,080 minutes.
At this point, please "turn" the page and do some Problems.
or
Continue on to Section 3: Multiplying by rounding off
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
