Lesson 15 Section 2
Parts, plural
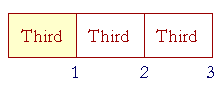
Let that long rectangle represent 3; and let us divide it into thirds, that is, into three equal parts; and let us shade one of them -- 1 out of 3.
1 is one third of 3.
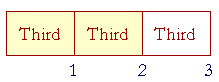
Two of the three rectangles have now been shaded. 2 out of 3. But each rectangle is a third part of the whole. Therefore those two rectangles together are two third parts of the whole. Or simply two thirds.
Those words, "two thirds," are to be taken literally, like two apples or two chairs. We are counting thirds:
One Third, two Thirds. 1, 2.
Now, 2 is not a part of 3, because 3 is not a multiple of 2. We say it is parts of 3, plural.
2 is two third parts of 3.
Notice how each number -- 2 out of 3 -- says its name. "Two thirds."
In Spanish, they say dos terceras partes -- two third parts -- which is literally true. But in English, unfortunately, we are not used to saying that.
| 5. | What does it mean to say that a smaller number is parts of a larger number? |
| It means that the larger number is not a multiple of the smaller. | |
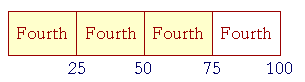
100 is not a multiple of 75. Therefore we say that 75 is parts of 100. It is three fourth parts, or simply three fourths.

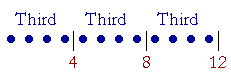
If the entire figure represents 15, then 5 is the third part of 15, and
10 is two third parts of 15.
If the entire figure represents 18, then 6 is the third part of 18, and
12 is two third parts of 18.
If the entire figure represents 21, then 7 is the third part of 21, and
14 is two third parts of 21.
And so on. Two thirds of a number are twice as much as one third.
Example 1. Fifths. Here is 10 divided into fifths, that is, into five equal parts:
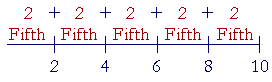
Each 2 is a Fifth. Let us count them.
2 is is the fifth part of 10.
4 is two fifth parts of 10.
6 is three fifth parts of 10.
8 is four fifth parts of 10.
And 10 is all five of its fifth parts.
Example 2. How much is two thirds of 12?
Answer. To name two thirds of 12, we must first name one third. But to name one third, we can simply divide by 3.
"12 divided by 3 is 4."
Two thirds will then be two times 4: 8.
We see, then, that to take two thirds of a number, divide it by 3, then multiply times 2.
Example 3. How much is two thirds of 27?
Answer. "3 goes into 27 nine times. Nine times 2 is 18."
(One third of 27 is 9. Two thirds are 18.)
Example 4. How much is three fourths of 28?
Answer. "4 goes into 28 seven times. Seven times 3 is 21."
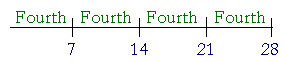
We can illustrate this with any number that has a fourth part, namely any multiple of 4. For example, 12, 40, 100:

One fourth of 12 is 3. Three fourths are 9.
One fourth of 40 is 10. Three fourths are 30
One fourth of 100 is 25. Three fourths are 75.
| 6. | How can we calculate parts of a number? |
| Four fifths of 15 | |
| Divide by the cardinal number that corresponds to the name of the part. Then multiply by the number of parts. | |
Example 5. How much is four fifths of 15?
Answer. "5 goes into 15 three times.. Three times 4 is 12."
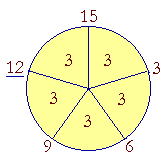
Each 3 is a fifth part of 15.
6 is two fifth parts of 15.
9 is three fifth parts of 15.
12 is four fifth parts, or simply four fifths, of 15.
Example 6. In a class of 32 students, five eighths are girls. How many boys are there?
Answer. The whole class is eight eighths. Therefore, if five eighths are girls, then the remaining three eighths are boys.
Now, one eighth of 32 -- 32 ÷ 8 -- is 4. Therefore three eighths will be three times 4: 12. There are 12 boys in the class.
Percent: Parts of 100%
We have seen that a percent is another way of naming a part. Since 100% is the whole (Lesson 4, Question 5), and since 50% is half of 100%, then 50% means half. 50% of 40 -- half of 40 -- is 20.
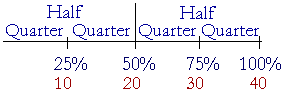
Since 25% is a quarter of 100%, then 25% is another way of saying a quarter. A quarter of 40 -- 25% of 40 -- is 10.
Since 75% is three quarters of 100%, then 75% means three quarters. 30 is 75% of 40.
Whichever part or parts the percent is of 100%, the percent means that part or those parts.
Fifths
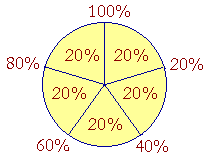
Let the circle represent 100%, and let us divide it into fifths, that is, into five equal parts -- into 20's. Each 20% is a fifth of the circle. Two fifths of the circle -- of 100% -- is 40% Three fifths is 60%. Four fifths is 80%.
That is what those percents mean:
20% means one fifth.
40% means two fifths.
60% means three fifths.
80% means four fifths.
100% is the whole; it is all five fifths.
Example 7. How much is 60% of 45?
Answer. 60% means three fifths.
"5 goes into 45 nine times. Nine times 3 is 27.
60% of 45 is 27.
Example 8. A scarf that sells for $35 is on sale at 40% off. How much do you pay?
Answer. "40% off" means that two fifths of the price will be subtracted. One fifth of 35 is 7. Therefore, two fifths are 14. You will pay $14 less:
$35 − $14 = $21.
You will pay $21.
More simply, since 40% of the price will be subtracted, then you will pay 60%. 60% -- or three fifths of $35 -- is three times $7, which is $21.
For more on percent, see Lesson 17.
Finally, we will state this theorem:
|
Each number is either a part of a larger number or parts of it. |
(Euclid, VII.4.)
We will illustrate that with each number less than 9. We will see that each number less than 9 is either a part of 9 or parts of 9.
Now, 9 units can be divided either into Ninths or Thirds:
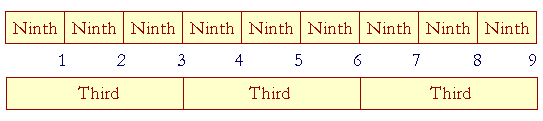
(If 9 is divided into Ninths, then it is divided into 1's. If 9 is divided into Thirds, then it is divided into 3's: 3, 6, 9.)
Let us now see how each number is related to 9.
1 is the ninth part -- or one ninth -- of 9.
2 is two ninth parts of 9.
(The point again is that each 1 is a ninth part of 9.)
3 is three ninths of 9 -- and also the third part of 9.
4 is four ninths of 9. Count them!
5 is five ninths of 9.
6 is six ninths -- and also two thirds -- of 9. 3 + 3.
7 is seven ninths of 9.
8 is eight ninths of 9.
Notice again how each number says its name:
1 is one ninth of 9.
2 is two ninths of 9.
3 is three ninths of 9.
The first number says its cardinal name. 9 says its ordinal name.
Each number less than 9, then, is either a part of 9 or parts of it. We can therefore express in words how each number is related to 9. We can say that 5, for example, is "five ninths" of 9.
Example 9. What relationship has 9 to 10?
Answer. If we divide 10 into 1's, then each 1 is a tenth part of 10.
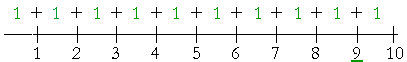
1 is one tenth of 10.
2 is two tenths of 10.
3 is three tenths of 10. And so on, until we come to 9:
9 is nine tenths of 10.
Again, the numbers 9 and 10 say their names. 9 says its cardinal name "nine." 10 says its ordinal name "tenth."
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
