5
Arc Length
The definition of radian measure
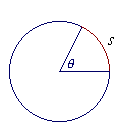
IT IS CONVENTIONAL to let the letter s symbolize the length of an arc, which is called arc length. We say in geometry that an arc "subtends" an angle θ; literally, "stretches under."
The circumference of a circle is an arc length. And the ratio of the circumference to the diameter is the basis of radian measure. That ratio is the definition of π.
| π | = | C D |
. |
Since D = 2r, then
| π | = | C 2r |
or,
| C r |
= | 2π | . |
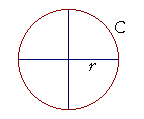 That ratio -- 2π -- of the circumference of a circle to the radius, is called the radian measure of 1 revolution, which are four right angles at the center. The circumference subtends those four right angles.
That ratio -- 2π -- of the circumference of a circle to the radius, is called the radian measure of 1 revolution, which are four right angles at the center. The circumference subtends those four right angles.
| Radian measure of θ = | s r |
Thus the radian measure is based on a ratio -- a number -- that is actually found in a circle. The radian measure is a real number that indicates the ratio of a curved line to a straight, of an arc to the radius. For the ratio of s to r does determine a unique central angle θ.
| Theorem. | In any circles the same ratio of arc length to radius | |
| determines a unique central angle that the arcs subtend. |
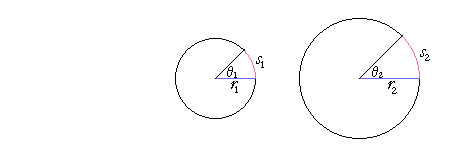
Proportionally,
![]()
if and only if
θ1 = θ2.
We will prove this theorem below.
Example 1. ;If s is 4 cm, and r is 5 cm, then the number ![]() , i.e.
, i.e. ![]() is the radian measure of the central angle.
is the radian measure of the central angle.
At that central angle, the arc is four fifths of the radius.
Example 2. An angle of .75 radians means that the arc is three fourths of the radius. s = .75r
Example 3. In a circle whose radius is 10 cm, a central angle θ intercepts an arc of 8 cm.

a) What is the radian measure of that angle?
Answer. According to the definition:
| θ = | s r |
= | 8 10 |
= .8 |
b) At that same central angle θ, what is the arc length in a circle whose radius is 5 cm?
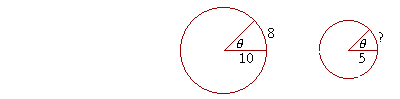
Answer. For a given central angle, the ratio of arc to radius is the same in all circles. Proportionally,
8 : 10 = ? : 5
5 is half of 10. The missing term will be half of 8. That arc is 4 cm.
Example 4.
a) At a central angle of 2.35 radians, what ratio has the arc to the radius?
Answer. That number is the ratio. The arc is 2.35 times the radius.
b) In which quadrant of the circle does 2.35 radians fall?
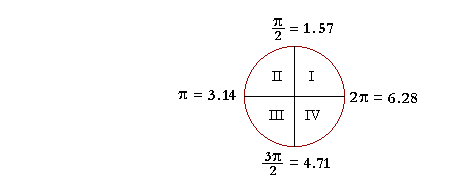
| Answer. Since π = 3.14, then | π 2 |
is half of that: 1.57. |
| 3π 2 |
= 3.14 + 1.57 = 4.71. |
An angle of 2.35 radians, then, is greater than 1.57 but less that 3.14. It falls in the second quadrant.
| c) | If the radius is 10 cm, and the central angle is 2.35 radians, then how long is the arc? |
Answer. We let the definition of θ,
| θ = | s r |
become a formula for finding s :
| s = rθ |
Therefore,
s = 10 × 2.35 = 23.5 cm
Because of the simplicity of that formula, radian measure is used exclusively in theoretical mathematics.
Problem 1.
| a) At a central angle of | π 5 |
, approximately what ratio has |
a) the arc to the radius? Take π![]() 3.
3.
| The radian measure | π 5 |
is that ratio. Taking π |
then the arc is approximately three fifths of the radius.
b) If the radius is 15 cm, approximately how long is the arc?
| s = rθ |
3 5 |
= 9 cm |
Problem 2. In a circle whose radius is 4 cm, find the arc length intercepted by each of these angles. Again, take π![]() 3.
3.
| a) | π 4 |
s = rθ |
3 4 |
= 3 cm |
| b) | π 6 |
s = rθ |
3 6 |
= 4· ½ = 2 cm |
| c) | 3π 2 |
s = rθ |
3· 3 2 |
| = 4· | 9 2 |
= 2· 9 = 18 cm |
d) 2π. (Here, the arc length is the entire circumference!)
| s = rθ = 4· 2π |
Problem 3. In which quadrant of the circle does each angle, measured in radians, fall? (See the figure above.)
| a) θ = 2 | 2 radians are more than | π 2 |
but less than π. (See the figure above.) Therefore, θ = 2 falls in the second quadrant.
| b) θ = 5 | 5 radians are more than | 3π 2 |
but less than 2π. (See the figure above.) Therefore, θ = 5 falls in the fourth quadrant.
| c) θ = 14 | 14 radians are more than 2 revolutions, |
but slightly less than 2¼: 6.28 + 6.28 = 12.56. (See the figure above.) Therefore, θ = 14 falls in the first quadrant.
An angle of 1 radian
An angle of 1 radian is defined to be a central angle whose subtending arc is equal to the radius.
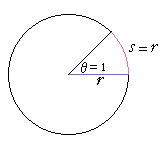
That is often cited as the definition of radian measure. But does such an angle actually exist? Is it possible to draw one -- a curved line equal to a straight line? It is possible to draw an angle of 2π radians. Those are the four right angles subtended by the circumference. We can also draw radian angles of
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and their multiples. Those are the angles that actually come up.
, and their multiples. Those are the angles that actually come up.
It is possible to define an angle of 1 radian. But again: Does such an angle exist?
See First Principles of Euclid's Elements, Commentary on the Definitions; see in particular that a definition asserts only how a word or a name will be used. It does not assert that what has been defined exists.
Proof of the theorem
In any circles the same ratio of arc length to radius
determines a unique central angle that the arcs subtend;
and conversely, equal central angles determine the same ratio
of arc length to radius.
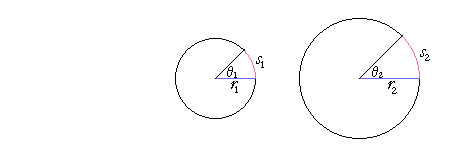
Proportionally,
![]()
if and only if
θ1 = θ2.
For,
![]()
if and only if
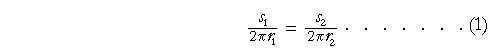
Now 2πr is the circumference of each circle. And each circumference is an "arc" that subtends four right angles at the center.
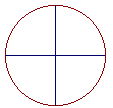
But in the same circle, arcs have the same ratio to one another as the central angles they subtend. (Theorem 16.) Therefore,
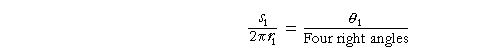
and
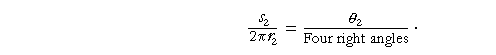
Therefore, according to line (1),
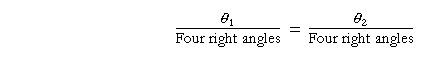
if and only if
θ1 = θ2.
Therefore, the same ratio of arc length to radius determines a unique central angle that the arcs subtend. Which is what we wanted to prove.
Next Topic: Definitions of the Trigonometric Functions
of an Acute Angle
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com