18
THE SQUARE OF A BINOMIAL
Perfect square trinomials
LET US BEGIN by learning about the square numbers. They are the numbers
1·1 2·2 3·3
and so on. The following are the first ten square numbers -- and their roots.
| Square numbers | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Square roots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 is the square of 1. 4 is the square of 2. 9 is the square of 3. And so on.
The square root of 1 is 1. The square root of 4 is 2. The square root of 9 is 3. And so on.
In a multiplication table, the square numbers lie along the diagonal.
The square of a binomial
(a + b)2
The square of a binomial comes up so often that the student should be able to write the final product immediately. It will turn out to be a very specific trinomial. To see that, let us square (a + b):
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2.
For, the outers plus the inners will be
ab + ba = 2ab.
The square of any binomial produces the following trinomial:
(a + b)2 = a2 + 2ab + b2
These will be the three terms:
1. The square of the first term of the binomial: a2
2. Twice the product of the two terms: 2ab
3. The square of the second term: b2
The square of a binomial is a essential form in the "multiplication table" of algebra.
See Lesson 8 of Arithmetic: How to square a number mentally, particularly the square of 24, which is the "binomial" 20 + 4.
Example 1. Square the binomial (x + 6).
Solution. (x + 6)2 = x2 + 12x + 36
x2 is the square of x.
12x is twice the product of x with 6. (x · 6 = 6x. Twice that is 12x.)
36 is the square of 6.
The square of a binomial is called a perfect square trinomial.
x2 + 12x + 36 is a perfect square trinomial.
Example 2. Square the binomial (3x − 4).
Solution. (3x − 4)2 = 9x2 − 24x + 16
9x2 is the square of 3x.
−24x is twice the product of 3x · −4. (3x · −4 = −12x. Twice that is −24x.)
16 is the square of −4.
Note: If the binomial has a minus sign, then the minus sign appears only in the middle term of the trinomial. Therefore, using the double sign ± ("plus or minus"), we can state the rule as follows:
(a ± b)2 = a2 ± 2ab + b2
This means: If the binomial is a + b, then the middle term will be +2ab; but if the binomial is a − b, then the middle term will be −2ab
The square of +b or −b, of course, is always positive. It is always +b2.
Example 3. (5x3 − 1)2 = 25x6 − 10x3 + 1
25x6 is the square of 5x3. (Lesson 13: Exponents.)
−10x3 is twice the product of 5x3 and −1. (5x3 times −1 = −5x3. Twice that is −10x3.)
1 is the square of −1.
The student should be clear that (a + b)2 is not a2 + b2, any more than (a + b)3 is equal to a3 + b3.
An exponent may not be "distributed" over a sum.
(See Topic 25 of Precalculus: The binomial theorem.)
Problem 1.
a) State in words the rule for squaring a binomial.
The square of the first term.
Twice the product of the two terms.
The square of the second term.
b) Write only the trinomial product: (x + 8)2 = x2 + 16x + 64
c) Write only the trinomial product: (r + s)2 = r2 + 2rs + s2
Problem 2. Write only the trinomial product.
| a) | (x + 1)2 = x2 + 2x + 1 | b) (x − 1)2 = | x2 − 2x + 1 | |
| c) | (x + 2)2 = x2 + 4x + 4 | d) (x − 3)2 = | x2 − 6x + 9 | |
| e) | (x + 4)2 = x2 + 8x + 16 | f) (x − 5)2 = | x2 − 10x + 25 | |
| g) | (x + 6)2 = x2 + 12x + 36 | h) (x − y)2 = | x2 − 2xy + y2 | |
Problem 3. Write only the trinomial product.
| a) | (2x + 1)2 = 4x2 + 4x + 1 | b) (3x − 2)2 = | 9x2 − 12x + 4 | |
| c) | (4x + 3)2 = 16x2 + 24x + 9 | d) (5x − 2)2 = | 25x2 − 20x + 4 | |
| e) | (x3 + 1)2 = x6 + 2x3 + 1 | f) (x4 − 3)2 = | x8 − 6x4 + 9 | |
| g) | (xn + 1)2 = x2n + 2xn + 1 | h) (xn − 4)2 = | x2n − 8xn + 16 | |
Example 4. Is this a perfect square trinomial: x2 + 14x + 49 ?
Answer. Yes. It is the square of (x + 7).
x2 is the square of x. 49 is the square of 7. And 14x is twice the product of x · 7.
In other words, x2 + 14x + 49 could be factored as
x2 + 14x + 49 = (x + 7)2
Note: If the coefficient of x had been any number but 14, this would not have been a perfect square trinomial.
Example 5 Is this a perfect square trinomial: x2 + 50x + 100 ?
Answer. No, it is not. Although x2 is the square of x, and 100 is the square of 10, 50x is not twice the product of x · 10. (Twice their product is 20x.)
Example 6 Is this a perfect square trinomial: x8 − 16x4 + 64 ?
Answer. Yes. It is the perfect square of x4 − 8.
Problem 4. Factor: p2 + 2pq + q2.
p2 + 2pq + q2 = (p + q)2
The left-hand side is a perfect square trinomial.
Problem 5. Factor as a perfect square trinomial -- if possible.
| a) | x2 − 4x + 4 = (x − 2)2 | b) | x2 + 6x + 9 = (x + 3)2 | |
| c) | x2 − 18x + 36 Not possible. | d) | x2 − 12x + 36 = (x − 6)2 | |
| e) | x2 − 3x + 9 Not possible. | f) | x2 + 10x + 25 = (x + 5)2 | |
Problem 6. Factor as a perfect square trinomial, if possible.
a) 25x2 + 30x + 9 = (5x + 3)2
b) 4x2 − 28x + 49 = (2x − 7)2
c) 25x2 − 10x + 4 Not possible.
d) 25x2 − 20x + 4 = (5x − 2)2
e) 1 − 16y + 64y2 = (1 − 8y )2
f) 16m2 − 40mn+ 25n2 = (4m − 5n)2
g) x4 + 2x2y2 + y4 = (x2 + y2)2
h) 4x6 − 10x3y4 + 25y8 Not possible.
i) x12 + 8x6 + 16 = (x6 + 4)2
j) x2n + 8xn + 16 = (xn + 4)2
Geometrical algebra
Here is a square whose side is a + b.
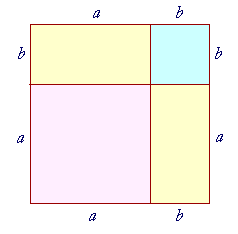
It is composed of
a square whose side is a,
a square whose side is b,
and two rectangles ab.
That is,
(a + b)2 = a2 + 2ab + b2.
Next Lesson: The difference of two squares
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
