Lesson 24
FRACTIONS
INTO DECIMALS
In this Lesson, we will answer the following:
| 1. | What is a decimal fraction? |
|
|
|
| It is a fraction whose denominator we do not write but we understand to be a power of 10. | |
| The number of decimal digits indicates the number of zeros in the denominator. | |
For the vocabulary of decimals, see Lesson 3.
Example 1.
| .8 | = | 8 10 |
One decimal digit; one 0 in the denominator. |
| .08 | = | 8 100 |
Two decimal digits; two 0's in the denominator. |
| .008 | = | 8 1000 |
Three decimal digits; three 0's in the denominator. |
| And so on. | |||
The number of decimal digits indicates the power of 10.
| Example 2. Write as a decimal: | 614 100,000 |
| Answer. | 614 100,000 |
= .00614 |
Five 0's in the denominator indicate five digits after the decimal point.
The five 0's in the denominator is not the number of 0's in the decimal![]()
Alternatively, in Lesson 10 we introduced the division bar, and in Lesson 4 we saw how to divide a whole number by a power of 10.
| 614 100,000 |
= | 614 ÷ 100,000 = .00614 |
Starting at the right of 614, separate five decimal digits.
| Example 3. Write this mixed number as a decimal: 6 | 49 100 |
| Answer. 6 | 49 100 |
= 6.49 |
The whole number 6 does not change. We simply replace the
| common fraction | 49 100 |
with the decimal .49. |
| Example 4. Write this mixed number with a common fraction: 9.0012 |
| Answer. 9.0012 = 9 | 12 10,000 |
Again, the whole number does not change. We replace the decimal
| .0012 with the common fraction | 12 10,000 | . The decimal .0012 has four |
decimal digits. The denominator 10,000 has four 0's.
This accounts for fractions whose denominator is already a power of 10.
| 2. | If the denominator is not a power of 10, how can we change the fraction to a decimal? |
|
| |
| Make the denominator a power of 10 by multiplying it or dividing it. | |
In fact, the decimal will be exact only if we can make the denominator a power of 10. See Section 2.
| Example 5. Write | 9 25 |
as a decimal. |
Solution. 25 is not a power of 10, but we can easily make it a power of 10 -- we can make it 100 -- by multiplying it by 4. We must also, then, multiply the numerator by 4.
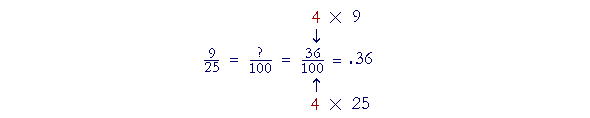
| Example 6. Write | 4 5 |
as a decimal. |
| Solution. | 4 5 |
= | 8 10 |
= .8 |
We can make 5 into 10 by multiplying it -- and 4 -- by 2.
| Example 7. Write as a decimal: | 7 200 |
| Solution. | 7 200 |
= | 35 1000 |
= .035 |
We can make 200 into 1000 by multiplying it -- and 7 -- by 5.
Alternatively,
| 7 200 |
= | 3.5 100 |
, on dividing both terms by 2, |
| = | .035 | , on dividing 3.5 by 100. | |
| Example 8. Write as a decimal: | 8 200 |
| Solution. | 8 200 |
= | 4 100 |
= .04 |
Here, we can change 200 into a power of 10 by dividing it by 2. We can do this because 8 also is divisible by 2.
Or, again,
| 8 200 |
= | _ 8 _ 2 × 100 |
= | 4 100 |
= .04 |
| Example 9. Write as a decimal: | 12 400 |
| Solution. | 12 400 |
= | 3 100 |
= .03 |
We can change 400 to 100 by dividing it -- and 12 -- by 4.
To summarize: We go from a larger denominator to a smaller by dividing (Examples 8 and 9); from a smaller denominator to a larger by multiplying (Example 5).
Example 10. Express 11 ÷ 20 as a decimal.
Solution. Upon using the division bar:
| 11 20 |
= | 55 100 |
= .55 |
We made 20 into 100 by multiply it by 5. We therefore had to multiply 11 by 5 also.
Example 11.
a) We know that 5% is 5 out of 100 (Lesson 4). .5%, then, is 5 out of how many?
Answer. We can change .5% into the decimal .005 (Lesson 4), which in
| turn is equal to the fraction | 5 1000 |
. |
| .5% | = | 5 1000 |
. |
Therefore, .5% is 5 out of 1000.
b) .05% is 5 out of how many?
| Solution. .05% = .0005 = | 5 10,000 |
. Therefore, .05% is 5 out of 10,000. |
Compare Lesson 18, Example 7.
Frequent decimals
In the actual practice of arithmetic, changing a fraction to a decimal is an extremely rare event. (We change a fraction to a percent directly: Lesson 27, Question 3.) The following are the only fractions whose decimal equivalents come up with any frequency. The student should know them.
| 1 2 |
1 4 |
3 4 |
1 8 |
3 8 |
5 8 |
7 8 |
| 1 5 |
2 5 |
3 5 |
4 5 |
| 1 3 |
2 3 |
| Let us begin with | 1 2 |
. |
| 1 2 |
= | 5 10 |
= .5 or .50. |
| Next, | 1 4 |
. But | 1 4 |
is half of | 1 2 |
. |
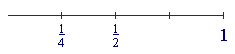
Therefore, its decimal will be half of .50 --
| 1 4 |
= .25 |
| As for | 3 4 |
, since | 3 4 |
= 3 × | 1 4 |
, then |
| 3 4 |
= 3 × .25 = .75 |
| Next, | 1 8 |
. But | 1 8 |
is half of | 1 4 |
. |
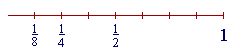
(Compare Lesson 15.)
Therefore its decimal will be half of .25 or .250 (Lesson 3) --
| 1 8 |
= .125 |
The decimals for the rest of the eighths will be multiples of .125.
Since 3 × 125 = 375,
| 3 8 |
= 3 × .125 = .375 |
| 5 8 |
will be 5 × | 1 8 |
= 5 × .125. |
5 × 125 = 5 × 100 + 5 × 25 = 500 + 125 = 625.
(Lesson 9) Therefore,
| 5 8 |
= .625 |
| Finally, | 7 8 |
= 7 × .125. |
7 × 125 = 7 × 100 + 7 × 25 = 700 + 175 = 875.
| 7 8 |
= .875 |
These decimals come up frequently. The student should know how to generate them quickly.
| Example 12. Write as a decimal: | 5 16 |
| Solution. | 5 16 |
will be 5 times | 1 16 |
. |
| Now, | 1 16 |
is half of | 1 8 |
(Lesson 15), which we saw is .125, or, .1250. |
| Therefore, | 1 16 |
= .0625. |
| 5 × 625 | = | 5 × 600 + 5 × 25 |
| = | 3000 + 125 | |
| = | 3125. | |
Therefore,
| 5 16 |
= .3125. |
Fifths
The student should also know the decimals for the fifths:
| 1 5 |
= | 2 10 |
= .2 |
The rest will be the multiples of .2 --
| 2 5 |
= | 2 × | 1 5 |
= 2 × .2 = .4 |
| 3 5 |
= 3 × .2 = .6 | |||
| 4 5 |
= 4 × .2 = .8 | |||
| Example 13. Write as a decimal: 8 | 3 4 |
| Solution. 8 | 3 4 |
= 8.75 |
The whole number does not change. Simply replace the common
| fraction | 3 4 |
with the decimal .75. |
| Example 14. Write as a decimal: | 7 2 |
Solution. First change an improper fraction to a mixed number:
| 7 2 |
= 3 | 1 2 |
= 3.5 |
"2 goes into 7 three (3) times (6) with 1 left over."
| Then repalce | 1 2 |
with .5. |
Example 15. How many times is .25 contained in 3?
| Answer. .25 = | 1 4 |
. And | 1 4 |
is contained in 1 four times. (Lesson 21.) |
| Therefore, | 1 4 |
, or .25, will be contained in 3 three times as many times. It will |
be contained 3 × 4 = 12 times.
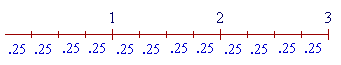
Example 16. How many times is .125 contained in 5?
| Answer. .125 = | 1 8 |
. And | 1 8 |
is contained in 1 eight times. Therefore, | 1 8 |
, |
or .125, will be contained in 5 five times as many times. It will be contained 5 × 8 = 40 times.
| As for | 1 3 |
and | 2 3 |
, neither one can be expressed exactly as a decimal. |
However,
| 1 3 |
.333 |
and
| 2 3 |
.667 |
Frequent percents
From the decimal equivalent of a fraction, we can easily derive the percent: Move the decimal point two digits right. Again, the student should know these. They come up frequently.
| 1 2 |
= | .50 | = | 50% | |||
| 1 4 |
= | .25 | = | 25% | |||
| 3 4 |
= | .75 | = | 75% | |||
| 1 8 |
= | .125 | = | 12.5% | (Half of | 1 4 |
. |
| See Lesson 27, Example 7.) | |||||||
| 3 8 |
= | .375 | = | 37.5%. | See above. | ||
| 5 8 |
= | .625 | = | 62.5% | |||
| 7 8 |
= | .875 | = | 87.5% | |||
| 1 5 |
= | .2 | = | 20% | |||
| 2 5 |
= | .4 | = | 40% | |||
| 3 5 |
= | .6 | = | 60% | |||
| 4 5 |
= | .8 | = | 80% | |||
In addition, the student should know
| 1 3 |
= 33 | 1 3 |
% |
| 2 3 |
= 66 | 2 3 |
% |
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
