Lesson 2
HOW TO READ AND WRITE
WHOLE NUMBERS
THE POWERS OF 10
In this Lesson, we will answer the following:
- What are the ten digits?
- Which numbers are the powers of 10?
- What are the names of the classes?
- How do we read a whole number, however large?
- To which place does each digit belong?
- What does it mean to write a number in expanded form?
- What is the relationship between the units of adjacent place value?
- How do we round off, or approximate, a whole number to a given place?
- How do we multiply a whole number by a power of 10?
- When a whole number ends in 0's, how do we divide it by a power of 10?
| 1. | What are the ten digits? |
| The ten symbols: 0 1 2 3 4 5 6 7 8 9 | |
Examples.
105 is a three-digit number. The digits are 1, 0, and 5.
28 ends in the digit 8.
$364 has the same digits as $3.64.
Those ten marks are also known as the Arabic numerals, because it was the Arab mathematicians who introduced them into Europe from India, where their forms evolved.
We saw in Lesson 1 that '364' is a numeral, which is a symbol for a number. A number is the actual collection of units.
The powers of 10
Number Ten is a collection of ten Ones.
![]()
One Hundred is a collection of ten Tens.

The number we call One Thousand is a collection of ten One Hundreds.

Ten One Thousands are called Ten Thousand.
The numbers in that sequence are called the powers of 10.
| 2. | Which numbers are the powers of 10? |
| They are the numbers produced when, starting with One, we continue collecting them into groups of 10. | |
| 10 Ones. 10 Tens. 10 Hundreds. 10 Thousands. And so on. |
|
Here are their names and numerals.
The Powers of 10
| Class of | One | 1 |
| Ones | Ten | 10 |
| Hundred | 100 | |
| Class of | One thousand | 1,000 |
| Thousands | Ten thousand | 10,000 |
| Hundred thousand | 100,000 | |
| Class of | One million | 1,000,000 |
| Millions | Ten million | 10,000,000 |
| Hundred million | 100,000,000 | |
| Class of | One billion | 1,000,000,000 |
| Billions | Ten billion | 10,000,000,000 |
| Hundred billion | 100,000,000,000 | |
Each power is composed of ten of the one above.
(The metric system is the system of measurement based on the powers of 10; see Lesson 4.)
Strictly, 1 is not a power of 10. The first power of 10 is 10 itself. Its numeral is a 1 followed by one 0. The second power of 10 is 100; it has two 0's. The third power has three 0's. And so on.
Notice how the names fall into groups of three:
One thousand, Ten thousand, Hundred thousand.
One million, Ten million, Hundred million.
Each group of three -- Ones, Tens, Hundreds -- is called a class.
Starting with Billions (bi for two), each class has a Latin prefix. To read a number more easily, we separate each class -- each group of three digits -- by commas.
Note that each class is 1000 times the previous class; the Thousands are 1000 times the Ones; the Millions are 1000 times the Thousands; and so on.
In Lesson 1 we showed how to read and write any number from 1 to 999, which are the numbers in the class of Ones. Together with knowing the sequence of class names, that is all that is necessary to be able to name or read any whole number.
| 4. | How do we read a whole number, however large? |
| 256,312,785,649,408,163 | |
| Starting from the left, read each three-digit group; then say the name of its class. | |
Example 1. Read this number:
256,312,785,649,408,163
Answer. Starting from the left, 256, read each three-digit group. Then say the name of the class.
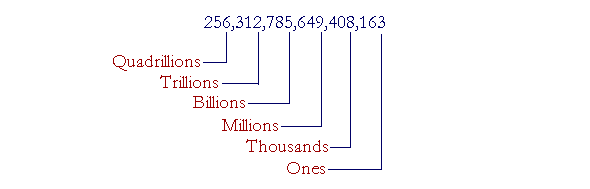
Say:
"256 Quadrillion, 312 Trillion, 785 Billion, 649 Million, 408 Thousand, 163."
Do not say the class name "Ones."
Example 2. To distinguish the classes, place commas in this number:
8792456
Answer. Starting from the right, place commas every three digits:
8,792,456
Read the number:
"8 million, 792 thousand, 456."
Example 3. Read this number: 7,000,020,002
Answer. "Seven billion , twenty thousand, two."
When a class is absent, we do not say its name; we do not say, "Seven billion, no million, ..."
Also, every class has three digits and so we must distinguish the following:
| 002 | "Two" |
| 020 | "Twenty" |
| 200 | "Two hundred" |
As for "and," in speech it is common to say "Six hundred and nine," but in writing we should reserve "and" for the decimal point, as we will see in the next Lesson. (For example, we should write $609.50 as "Six hundred nine dollars and fifty cents." Not "Six hundred and nine dollars.")
Example 4. Write in numerals:
Four hundred eight million, twenty-nine thousand, three hundred fifty-six.
Answer. Pick out the classes: "million", "thousand". Each class (except perhaps the first class on the left) has exactly three digits:
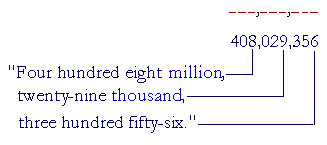
Example 5. Write in numerals:
Five billion, sixteen thousand, nine.
Answer. After the billions, we expect the millions, but it is absent. Therefore write
5,000,016,009
Again, we must write "sixteen thousand" as 016; and "nine" as 009; because each class must have three digits. The exception is the class on the extreme left. We may write "Five" as 5 rather than 005.
When writing a four-digit number, such as Four thousand five hundred, it is permissible to omit the comma and write 4500. In fact, we often read that as "Forty-five hundred." But when a number has more than four digits, then for the sake of clarity we should always place the commas.
Example 6. Distinguish the following:
| a) Two hundred seventeen million | b) Two hundred million seventeen |
| Answers. | |
| a) 217,000,000 | b) 200,000,017 |
At this point, please "turn" the page and do some Problems.
or
Continue on to Section 2: Place value numeration
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com

