The Topics | Home
2
THE CIRCLE


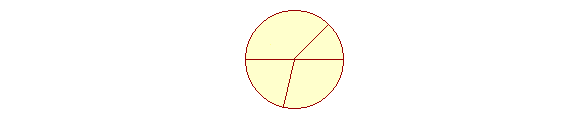
A CIRCLE is a plane figure bounded by one line, called the circumference, such that all straight lines drawn from the center to the circumference are equal to one another.
A straight line from the center to the circumference is a called a radius. A diameter is a straight line through the center and terminating in both directions on the circumference.
A radius, then, is half of a diameter; or, equivalently, a diameter is twice a radius:
D = 2r.
The definition of π
The student no doubt knows a value for the famous irrational number π — 3.14 — but that is not its definition. What, in fact, is the meaning of the symbol "π"?
Any two quantities of the same kind have a ratio to one another, a relationship with respect to relative size. The circumference C and
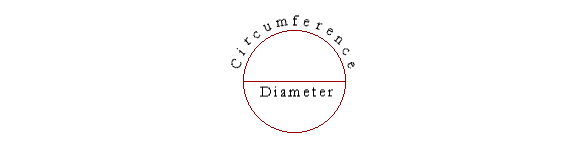
diameter D are both lengths, and so they have a ratio to one another. That ratio -- how many times longer C is than D -- is called π.
C = πD.
The circumference C varies directly as the diameter D. If the diameter doubles, the circumference will double; and so on. π is the constant of proportionality.
Since ancient times, it was known that π is a bit more than 3. In the third century B. C., Archimedes of Syracuse proved that π is more than 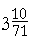 , but less than , but less than 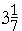 . .
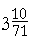 < π < < π < 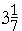 . .
In modern decimals:
3.140845 < π < 3.142857
It was not until the 18th century that it was proved that π is irrational. And when the ratio of two quantities is irrational, then for practial purposes we have to approximate it as a rational number.
C = πD 3.14159 D. 3.14159 D.
It should be intuitively clear that π cannot be rational, because it signifies the ratio of a curved line to a straight. And to name such a ratio exactly is impossible.
We will see how to approximate π in the next Topic.
In any case, since
then we use that as a formula for calculating the circumference of a circle.
Or, since D = 2r,
C = π· 2r = 2πr.
Problem 1. Calculate the circumference of each circle. Take π = 3.14.
To see the answer, pass your mouse over the colored area. To cover the answer again, click "Refresh" ("Reload").
a) The diameter is 5 cm.
3.14 × 5 = 15.7 cm
b) The radius is 5 cm.
3.14 × 2 × 5 = 3.14 × 10 = 31.4 cm
Problem 2.
The average distance of the earth from the sun is approximately 93 million miles; assuming that the earth's path around the sun is a circle, approximately how many miles does the earth travel in a year?
C = π × 2r = 3.14 × 2 × 93 million = 584.04 million miles.

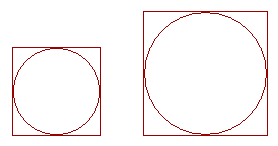
Circles are to one another as their circumscribed squares.
(After Euclid, XII, 2.)
The theorem asserts that the area of a circle varies directly as the area of the circumscrbed square. Therefore there is a constant of proportionality.
Now the side of a circumscribed square is the diameter D; hence its area is D2. When we prove that the area of a circle is
then we see that that constant is 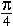 . .
We are about to see that 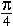 may be more fundamental than π. For it is also the constant that relates the circumference of a circle to the perimeter of the circumscribed square. may be more fundamental than π. For it is also the constant that relates the circumference of a circle to the perimeter of the circumscribed square.
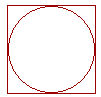
Again, the side of a circumscribed square is equal to the diameter D. Therefore its perimeter is 4D. Hence the ratio of the circumference C to the perimeter is 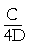 . And since . And since 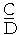 has been called π, then has been called π, then
That is,
We now have one of the most remarkable theorems.

The circumference of a circle is to the perimeter
of the circumscribed square, as the area
of the circle is to the area of the square.
As the boundary is to the boundary, so the area is to the area.
The constant of proportionality is 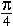 . .
Finally, it is possible to prove the following:
π
4 |
= 1 − |
1
3 |
+ |
1
5 |
− |
1
7 |
+ |
1
9 |
− |
1
11 |
+ |
. . . |
If we took just the first two terms of that series, that would tell us that the circle is approximately two thirds of the square. If we took three terms, we would know that the circle is appoximately thirteen fifteenths of the square. Each term brings us a little more and then a little less than the actual ratio that the circle has to the circumscribed square. But we will never be able to name that ratio exactly. 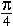 is an irrational number. is an irrational number.
If there is anything in mathematics that deserves to be called beautiful, it is here. (Note: There is no such simple series for π.) We find such beauty when geometry is reflected by arithmetic. We discover those relationships in those archetypal forms. We do not invent them.
Next Topic: Angles and their measurement
The Topics | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
|