Lesson 28
PERCENTS ARE RATIOS
In this Lesson, we will answer the following:
The very first Lesson on Percent is Lesson 4.
Now every statement of percent can be expressed verbally in this way:
"One number is some percent of another number."
"____ is ____% of ____."
We call that the standard form. For example,
8 is 50% of 16.
Every statement of percent therefore involves three numbers. 8 is called the Amount. 50% is the Percent. 16 is called the Base. The Base always follows "of." And in the standard form, it will be the last number.
The standard form is the same as that in which we express a ratio, which is a relationship between two numbers.
8 is half of 16.
All relationships have names. "Cousin." Mom." "Boyfriend." The name of the relationship—the ratio—that 8 has to 16 is "half." In the language of percent, the name of that relationship is "50%."
In this Lesson, we emphasize going back and forth between those two languages: percent and ratio.
| How do percents name ratios? | |
|
Whatever ratio the percent has to 100%, that is the relationship being named. |
|
| Conversely, whatever ratio is named the percent has that same ratio to 100%. |
|
What ratio is each of the following?
50%.
Half. Because 50 is half of 100.
25%.
A quarter, or a fourth. Because 25 is a quarter of 100.
| 33 | 1 3 |
% | . |
| A third. Because if we divide 100 by 3, we get 33 | 1 3 |
. (Lesson 16.) |
| 33 | 1 3 |
is a third of 100. |
The tenth part. Because 10 is the tenth part 100.
200%.
Two times, or twice as much. Because 200 is two times 100.
250%.
Two and a half times. Because 250 is two and a half times 100. (Lesson 18, Question 6.)
1000%.
Ten times. Because 1000 is ten times 100.
Whatever ratio the percent has to 100 percent, that is the ratio being named.
Upon completing Problem 1 at the end of this Lesson, the student will have a firm foundation in the language of percent.
*
Again:
The Amount is some Percent of the Base.
A percent problem consists of being given two of those numbers, and having to find the third.
The Amount
Example 1. How much is 100% of 12?
Answer. 12. 100% is all.
Example 2. How much is 200% of 12?
Answer. 24. 200% is twice as much as 100%.
Example 3. How much is 300% of 12?
Answer. 36. 300% is three times 100%.
Example 4. How much is 50% of 12?
Answer. Translate immediately into the language of ratio: "How much is half of 12?" Answer: 6.
| Example 5. How much is 33 | 1 3 |
% of 12? |
Translate: "How much is a third of 12?" A third of 12 is 4.
Example 6. How much is 350% of 12?
Translate: "How much is a three and a half times 12?" (350% = 300% + 50%: Three times plus half.)
Three times 12 is 36. Half of 12 is 6. 36 + 6 = 42.
We see that more than 100% of 12 is more than 12,
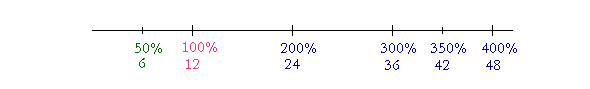
while less than 100% will be less.
Example 7. How much is 1% of $512?
Translate: "How much is a hundredth of $512?" (1% means a hundredth because 1 is the hundredth part of 100.) To find a hundredth of a number, divide it by 100. To divide a whole number by 100, separate two decimal digits:
1% of $512 is $5.12.
Example 8. How much is 2% of $512?
Answer. 2% is twice as much as 1%. 1% of $512 is $5.12. Therefore
2% is 2 × $5.12 = $10.24.
Example 9. How much is 10% of $434?
Translate: "How much is a tenth of $434?" (10% means a tenth, because 10 is a tenth of 100.) To find a tenth of a number, divide it by 10. To divide a whole number by 10, separate one decimal digit:
$434 ÷ 10 = $43.4
We write money however with two decimal digits. Therefore report 10% as
$43.40.
See Lesson 4, Question 7.
Example 10. How much is 20% of $142?
Answer. 20% is twice as much as 10%. 10% of $142 is $14.20. Therefore 20% is $28.40.
For a simple way to calculate 25%, 5%, and 15%, see Lesson 16, Questions 10, 12, and 14.
For more problems in finding a percent of a number, see Lesson 29.
The Base
Example 11. 7 is 25% of _?_
Answer. The Base -- the number that follows of -- is missing.
Translate:
"7 is a quarter of what number?"
7 is a quarter of 28.
In fact, every number is a quarter, or 25%, of 4 times itself.
6 is 25% of 24.
9 is 25% of 36.
$105 is 25% of $420.
And so on.
Example 12. 10 is 20% of _?_
Translate: "10 is the fifth part of what number?" (20% means the fifth part, because 20 is the fifth part of 100.)
10 is the fifth part of 50.
Every number is the fifth part of 5 times itself.
Example 13. 10% of what number is 59?
Answer. In standard form:
59 is 10% of what number?
Translate:
"59 is the tenth part of what number?"
59 is the tenth part of 10 × 59 = 590.
This Example illustrates that it is always a good idea to express any percent problem in the standard form.
Example 14. 300% of what number is 15?
In standard form:
15 is 300% of what number?
Translate:
"15 is the three times what number?"
15 is three times 5.
Example 15. 280 is 1000% of _?_
Translate: "280 is the ten times what number?"
280 is ten times 28.
For more problems in finding the Base, see Lesson 29.
The Percent
Example 16. 48 is what percent of 48?
Answer. 100%. 100% is the whole thing!
Example 17. 9 is what percent of 36?
Answer. To ask
9 is what percent of 36?
is the same as asking
9 has what ratio to 36?
Percents are ratios.
Now,
9 is a fourth of 36.
Therefore,
9 is 25% of 36.
25% means a fourth, or a quarter.
Example 18. 35 is what percent of 7?
Translate: "35 has what ratio to 7?"
35 is five times 7.
The percent, then, will be five times 100%:
35 is 500% of 7.
In every case,
The percent has that same ratio to 100%.
Example 19. Same digits. $2.50 is what percent of $250?
Answer. The digits are the same: 2, 5, 0 -- but $2.50 has two decimal digits. It is $250 divided by 100:
$2.50 = $250 ÷ 100.
(Lesson 4.) Therefore,
$2.50 is 1% of $250.
Compare Lesson 15, Examples 5 and 6.
Percent continues in Lesson 30.
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section: Percent increase or decrease.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
