Lesson 29 Section 3
To find the Base
the number that follows "of"
Example 1. 7 is 25% of what number?
Here, the Base is missing, the number that follows of. This is an elementary problem in finding the Base. It's Example 11 in Lesson 28.
| Example 2. 14 is 66 | 2 3 |
% of what number? | (See Lesson 16.) |
Solution 1. The problem asks:
14 is two thirds of what number?
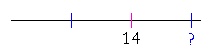
But if 14 is two thirds, then half of 14 is one third. Half of 14 is 7. And 7 is one third -- of 21.
| 14 is 66 | 2 3 |
% of 21. |
Any number will be two thirds of one and a half times itself.
Solution 2. If 14 is two thirds of some number, then proportionally:
As 2 is to 3, then 14 is to ?
2 : 3 = 14 : ?
"2 goes into 14 seven times. Seven times 3 is 21."
2 : 3 = 14 : 21.
14 is two thirds of 21.
Compare Lesson 18, Examples 5 and 6.
Example 3. 30 is 60% -- three fifths -- of what number?
Solution 1. If 30 is three fifths of some number,
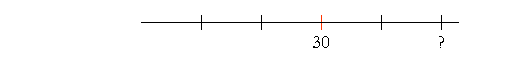
then a third of 30 is one fifth.
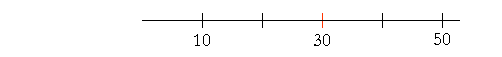
A third of 30 is 10. And 10 is one fifth -- of 50.
30 is 60% of 50.
Solution 2. If 30 is three fifths of some number, then proportionally:
3 : 5 = 30 : ?
To produce 30, 3 has been multiplied by 10. Therefore 5 must also be mutiplied by 10.
3 : 5 = 30 : 50.
30 is three fifths -- 60% -- of 50.
Example 4. 27 is 75% -- three fourths -- of what number?
Solution. Proportionally:
3 : 4 = 27 : ?
"3 goes into 27 nine times. Nine times 4 is 36.
3 : 4 = 27 : 36..
27 is three fourths -- 75% -- of 36.
It turns out that we will always be able to find the Base by the method of proportions, which is an instance of The Rule of Three.
| As the Percent is to 100 so the Amount is to the Base. |
| P : 100 = A : B. |
Example 5. $36 is 4% of how much?
| Solution. | 4 : 100 = $36 : ? |
"4 goes into 36 nine times. Nine times 100 is 900."
4 : 100 = $36 : $900.
$36 is 4% of $900.
Example 6. 42 is 6% of what number? Check your answer.
| Solution. | 6 : 100 = 42 : ? |
42 is seven times 6. Therefore, the missing term must be seven times 100.
6 : 100 = 42 : 700.
42 is 6% of 700.
Here is the check:
1% of 700 is 7. Therefore, 6% is 6 × 7 = 42.
Example 7. 8% of what number is 20?
| Solution. | 8 : 100 = 20 : ? |
On dividing both terms on the left by 4
2 : 25 = 20 : ?
"2 goes into 20 ten times. Ten times 25 is 250.
2 : 25 = 8 : 100 = 20 : 250.
20 is 8% of 250.
Check: 1% of 250 = 2.5
| Therefore, 8% of 250 = 8 × 2.5 | = | 2.5 × 8 (Two and a half times 8) |
| (Lesson 27, Examples 10 and 11) | ||
| = | 20. | |
Example 8. 9 is 15% of what number?
| Solution. | 15 : 100 =9 : ? |
On dividing by 5:
3 : 20 = 9 : ?
3 has been multiplied by 3. Therefore, 20 must be multiplied by 3:
3 : 20 =9 : 60.
9 is 15 % of 60.
(10% of 60 is 6. 5% is 3. 6 + 3 = 9.)
Example 9. 24 is 150% of what number?
| Solution. | 150 : 100 =24 : ? |
On dividing by 50:
3 : 2 = 24 : ?
"3 goes into 24 eight times. Eight times 2 is 16."
3 : 2 =24 : 16.
24 is 150 % of 16.
Check: 24 is 150% of -- 1½ times -- 16. (16 + 8 = 24.)
(Lesson 16.)
Example 10. Maria is retired and withdraws money from her retirement account. But a tax of 20% is automatically withheld. If she needs $1200, how much must she actually request?
Solution 1.. Since 20% will be withheld, Maria will receive 80% of her request. So the question is: $1200 is 80% of how much?
80 : 100 = 4 : 5 = 1200 : ?
4 has been multiplied by 300. Therefore, 5 must be multiplied by 300:
4 : 5 =1200 : 1500.
$1200 is 80% of $1500.
In other words, since 5 is one and a quarter times 4, then Maria must always request one quarter more than what she needs. One quarter of $1200 is $300. Therefore she must request $1200 + $300 = $1500.
It is then a simple matter to see that 20%, or a fifth, of $1500 is $300, so that her net amount will in fact be $1200.
Solution 2. We have seen that to find the Amount, we multiply.
Amount = Base × Percent
Therefore, according to the relationship between multiplication and division, to find the Base, we divide.
Base = Amount ÷ Percent
In this Example, we are to divide 1200 by 80%, or 4/5. But we have seen that division is multiplication by the reciprocal. That will result in multiplying by 5/4 or 1¼.
1¼ × $1200 = $1200 + $300 =$1500.
Example 12. Michelle paid $82.68 for a pair of shoes -- but that included a tax of 6%. What was the actual price of the shoes before the tax?
Solution. This is Example 7: Percent with a Calculator.
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
