Lesson 27
THE MEANING OF MULTIPLYING FRACTIONS
FRACTIONS INTO PERCENTS
PARTS OF FRACTIONS
In this Lesson, we will answer the following:
In the previous Lesson we simply stated the rule for multiplying fractions. In this Lesson we want to understand where that rule comes from. It comes from what multiplying by a fraction means.
First, in Lesson 15 we saw what "the third part", or "one third" of a number means. "One third of 15," for example, is 5.
In symbols, "One third of 15" will be written as multiplication:
| 1 3 |
× | 15. |
That is what multiplication by a fraction means.
| 1. | What does it mean to multiply a number by a fraction? | ||
|
|||
| It means to take that part of the number. | |||
| 1 2 |
× 8 means One half of 8, which is 4. |
| 1 4 |
× 20 means One fourth of 20, which is 5. |
| 3 4 |
× 20 means Three fourths of 20, which is 15. |
| .15 × 20 means | Fifteen hundredths of 20, which is 3. |
| (One hundredth of 20 is .2.) |
For, according to the meaning of multiplication, we are to repeatedly add the multiplicand as many times as there are 1's in the multiplier. In the multiplier ½ there is one half of 1. Therefore we are to add the multiplicand 8 one half a time. We are to take one half of 8.
Also, although "½ × 8" looks like multiplication, there is nothing to multiply. "½ × 8" is a symbolic abbreviation for "One half of 8." And to calculate it, we have to divide. (Lesson 15.) We can now begin to see why we have the cancelation rules.
This is another use for fractions apart from numbers we need for measuring: Multiplication by a fraction signifies a part of the multiplicand.
And so the symbolic statement, "4 = ½ × 8," expresses the ratio of 4 to 8: "4 is one half of 8."
For the most general definition of multiplication, see Section 3.
Example 1. Calculate ![]() × 21 "Two thirds of 21." (We may read "
× 21 "Two thirds of 21." (We may read "![]() × 21" as "Two thirds of 21" rather than "Two thirds times 21.")
× 21" as "Two thirds of 21" rather than "Two thirds times 21.")
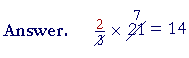
One third of 21 is 7 -- "3 goes into 21 seven (7) times." 2 × 7 = 14.
If the problem were just to evaluate Two thirds of 21, the student should not have to resort to writing ![]() × 21.
× 21.
Simply say, "One third of 21 is 7. So two thirds are 14." (Lesson 15.) The point of this Lesson is to explain what it means to multiply by a fraction.
Problem. ![]() × 32. What does that mean?
× 32. What does that mean?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
"Five eighths of 32."
Calculate it.
"One eighth of 32 is 4. So five eighths are five times 4: 20."
Compare Lesson 15, Example 5.
Example 2. Calculate ![]() × 5. "Three fourths of 5."
× 5. "Three fourths of 5."
Solution. Although 5 is not exactly divisible by 4, we can still take its fourth part -- by dividing by 4:
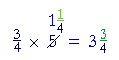
"4 goes into 5 one (1) time with 1 left over."
One fourth of 5 is 1![]() ; therefore, three fourths are 3 × 1
; therefore, three fourths are 3 × 1![]() = 3
= 3![]() .
.
(Lesson 26.)
Alternatively, we can multiply first:
![]() × 5 =
× 5 = ![]() = 3
= 3![]() .
.
"4 goes into 15 three (3 ) times (12) with 3 left over."
We see:
We may take a part first or multiply first.
Example 3. You are going on a a trip of four miles, and you have gone two thirds of the way. How far have you gone?
Solution. We must take two thirds of 4.
"One third of 4 is 1![]() ."
."
![]() = 1
= 1![]() .
.
"Therefore two thirds are 2 × 1![]() = 2
= 2![]() ."
."
You have gone 2![]() miles.
miles.
Example 4. How much is a fifth of 3?
Solution. While we could write ![]() × 3 =
× 3 = ![]() , we know that to find a fifth of a number, we divide by 5. And 3 ÷ 5 is
, we know that to find a fifth of a number, we divide by 5. And 3 ÷ 5 is ![]() . Lesson 11, Example 17.
. Lesson 11, Example 17.
Therefore, we could know immediately:
A fifth of 3 is ![]() .
.
Example 5. How much is a fourth of 9 gallons?
Answer. ![]() = 2
= 2![]() gallons.
gallons.
"4 goes into 9 two times with 1 left over."
Example 6. Calculator problem. Tim and his business partner invested $71,000 in a property. Tim invested $51,000, and his partner, $20,000.
They had to sell the property at a loss for $48,000. If each one receives the same fraction that they invested, how much will each one recieve?
Solution. First, what fraction of the $71,000 did Tim invest? 51,000 is what fraction of 71,000? It is ![]() of it. (Lesson 20. Note that we may omit the final 0's.)
of it. (Lesson 20. Note that we may omit the final 0's.)
We are to find that same fraction of 48,000:
![]() × 48,000.
× 48,000.
Press
| 5 | 1 | ÷ | 7 | 1 | × | 48000 | = |
See:
| 34478.872 |
Tim's share will be $34,479. (Lesson 12.) Therefore his partner's share to make up the difference will be
$48,000 − $34,479 = $13,521.
Example 7 How much money is 64 quarters?
Answer. 64 quarters would be 64 × $.25. But according to the order property of multiplication,
64 × .25 = .25 × 64.
Now .25 is the decimal for ¼. Therefore we can evaluate 64 quarters by taking one quarter of 64. And we can do that by taking half of half. (Lesson 16.)
Half of 64 is 32. Half of 32 is 16. Therefore 64 quarters are $16.
Example 8. A slot machine at a casino paid 93 quarters. How much money is that?
Answer. To find a quarter of 93, divide 93 by 4. We can easily do that mentally by decomposing 93 into multiples of 4. For example:
93 = 80 + 12 + 1.
On dividing each term by 4, we have
20 + 3 + ¼ = 23¼.
93 quarters, then, are $23.25.
Example 9. A recipe calls for 3 cups of flour and 4 cups of milk. Proportionally, how much milk should you use if
a) you use 1½ cups of flour? b) you use 2 cups of flour?
c) you use 2½ cups of flour?
Answers.
a) 1½ cups flour are half of 3 cups. Therefore you should use half as
a) much milk. You should use 2 cups.
b) 2 cups flour are two thirds of 3 cups. That is the ratio of 2 cups to 3. b) Therefore you should use two thirds as much milk.
![]() × 4 =
× 4 = ![]() = 2
= 2![]() cups milk.
cups milk.
c) What ratio has 2½ cups of flour to the original 3 cups?
On expressing 2½ as the improper fraction ![]() , then on cross-multiplying:
, then on cross-multiplying:
![]() is to 3 as 5 is to 6.
is to 3 as 5 is to 6.
2½ cups are five sixths of 3 cups.
Therefore, you should use five sixths of 4 cups of milk.
![]() × 4 =
× 4 = ![]() = 3
= 3![]() = 3
= 3![]() cups of milk.
cups of milk.
| 2. | How do we multiply a whole number by a mixed number? | ||
| 2½ × 8 | |||
| Multiply by the whole number of the mixed number, then multiply by the fraction. It is not necessary to change to an improper fraction. | |||
In Lesson 16, Question 3, we saw this as a mixed number of times.
Example 10. 2½ × 8.
| Answer. 2½ × 8 | = 2 × 8 + ½ × 8 |
| ("Two times 8 + Half of 8") |
| Answer. 2½ × 8 | = 16 + 4 |
| Answer. 2½ × 8 | = 20. |
In multiplication, when one of the numbers is a whole number, it is not necessary to change to an improper fraction.
(In that regard, see the previous Lesson, Question 2.)
Example 11. 5![]() × 7.
× 7.
Answer. "5 times 7 is 35. A third of 7 is 2![]() ." (Lesson 20, Problem 16.)
." (Lesson 20, Problem 16.)
"35 plus 2![]() is 37
is 37![]() ."
."
Example 12. Mental calculation. What is the price of 12 items at $3.25 each?
Answer. 12 × $3.25 is equal to $3.25 × 12, or, 3¼ × 12:
| 3¼ × 12 | = Three times 12 + A quarter of 12 |
| 3¼ × 12 | = 36 + 3 |
| 3¼ × 12 | = $39. |
Example 13. Multiplying by numbers ending in 5. Calculate mentally: 75 × 6.
Answer. Rather than 75 × 6, let us do
7.5 × 6
that is,
7½ × 6.
7½ × 6 = 42 + 3 = 45.
Now, by replacing 75 with 7.5, we divided by 10. (Lesson 4,
Question 5.) Therefore, to name the right answer we must multiply 45 by 10:
75 × 6 =450.
Example 14. 35 × 16
Answer. 3.5 × 16 = 48 + 8 = 56. Therefore,
35 × 16 = 560.
| 3. | How can we express a fraction as a percent? |
|
|
|
| Multiply it times 100%. | |
That is how to change any number to a percent. (Lesson 4.)
Example 15. Express ![]() as a percent. Express
as a percent. Express ![]() as a percent.
as a percent.
Solution. 100% is the whole. Therefore, take one eleventh of 100%:
![]() × 100% = 100% ÷ 11.
× 100% = 100% ÷ 11.
"11 goes into 100 nine (9) times (99) with 1 left over."
![]() = 9
= 9![]() %.
%.
As for ![]() , it is five times
, it is five times ![]() (Lesson 21):
(Lesson 21):
5 × 9![]() % = 45
% = 45![]() %.
%.
(See the previous Lesson, Question 2.)
We will go into this again in Lesson 30, Question 3.
For the most frequent percent equivalents, see Lesson 24.
The order of taking a part and multiplying
To calculate
| 3 4 |
× 5 "Three fourths of 5," |
we may either take the fourth part first, or multiply by 3 first. That is,
Three fourths of 5 = 3 × One fourth of 5 = One fourth of 3 × 5.
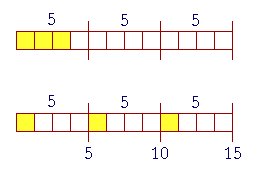
In both figures, each 5 has been divided into fourths.
The upper figure shows 3 × One fourth of 5, that is, Three fourths of 5.
The bottom figure shows one fourth of three 5's. And they are equal.
Therefore to multiply a whole number by a fraction, we may either take the part first or multiply first.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2: Parts of fractions.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
