skill

S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

Lesson 24

FRACTIONS
INTO DECIMALS


In this Lesson, we will answer the following:

  1. What is a decimal fraction?
  2. If the denominator is not a power of 10, how can we change the fraction to a decimal?

    Frequent decimals: Half, quarters, eighths, fifths, thirds.

    Frequent percents.

    Section 2

  3. What is a general method for expressing a fraction
    as decimal?

    Exact versus inexact decimals.
 1.   What is a decimal fraction?
 
decimals
 
  It is a fraction whose denominator we do not write but we understand to be a power of 10.
  The number of decimal digits indicates the number of zeros in the denominator.
 

For the vocabulary of decimals, see Lesson 3.

Example 1.   

.8 =  8 
10		   One decimal digit; one 0 in the denominator.
.08 =   8  
100		   Two decimal digits; two 0's in the denominator.
.008 =    8   
1000		   Three decimal digits; three 0's in the denominator.
And so on.

The number of decimal digits indicates the power of 10.


  Example 2.    Write as a decimal:       614  
100,000
  Answer.       614  
100,000		  = .00614

Five 0's in the denominator indicate five digits after the decimal point.

The five 0's in the denominator is not the number of 0's in the decimalexclamation

Alternatively, in Lesson 10 we introduced the division bar, and in Lesson 4 we saw how to divide a whole number by a power of 10.

   614   
100,000		   =   614 ÷ 100,000 = .00614

Starting at the right of 614, separate five decimal digits.

  Example 3.    Write this mixed number as a decimal:  6  49  
100
  Answer.   6  49 
100		  = 6.49

The whole number 6 does not change. We simply replace the

  common fraction   49 
100		  with the decimal  .49.

  Example 4.   Write this mixed number with a common fraction:  9.0012
  Answer.   9.0012 = 9    12   
10,000

Again, the whole number does not change.  We replace the decimal

  .0012 with the common fraction     12   
10,000 		.  The decimal  .0012  has four

decimal digits.  The denominator 10,000 has four 0's.

This accounts for fractions whose denominator is already a power of 10.
 
 2.   If the denominator is not a power of 10, how can we change the fraction to a decimal?
decimals
  Make the denominator a power of 10 by multiplying it or dividing it.
 

In fact, the decimal will be exact only if we can make the denominator a power of 10.  See Section 2.

  Example 5.   Write   9 
25		  as a decimal. 

Solution.  25 is not a power of 10, but we can easily make it a power of 10 -- we can make it 100 -- by multiplying it by 4.  We must also, then, multiply the numerator by 4.

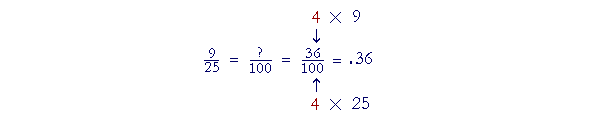
decimals
  Example 6.   Write  4
5		  as a decimal.
  Solution.    4
5		  =   8 
10		  = .8

We can make 5 into 10 by multiplying it -- and 4 -- by 2.


  Example 7.   Write as a decimal:     7  
200
  Solution.      7  
200		  =    35  
1000		  = .035

We can make 200 into 1000 by multiplying it -- and 7 -- by 5.

Alternatively,

  7  
200		   =    3.5
100		 , on dividing both terms by 2,
 
    =   .035 ,  on dividing 3.5 by 100.
  Example 8.   Write as a decimal:     8  
200
  Solution.      8  
200		  =    4 
100		  = .04

Here, we can change 200 into a power of 10 by dividing it by 2.  We can do this because 8 also is divisible by 2.

Or, again,

  8  
200		   =     _ 8 _  
2 × 100		   =     4  
100		   =  .04
  Example 9.   Write as a decimal:    12  
400
  Solution.     12  
400		  =    3 
100		  = .03

We can change 400 to 100 by dividing it -- and 12 -- by 4.

To summarize:  We go from a larger denominator to a smaller by dividing (Examples 8 and 9);  from a smaller denominator to a larger by multiplying (Example 5).

Example 10.   Express 11 ÷ 20 as a decimal.

Solution.  Upon using the division bar:

11
20		 =  55 
100		 = .55

We made 20 into 100 by multiply it by 5. We therefore had to multiply 11 by 5 also.

Example 11.

a)  We know that 5% is 5 out of 100 (Lesson 4).  .5%, then, is 5 out of how many?

Answer.   We can change .5% into the decimal .005 (Lesson 4), which in

  turn is equal to the fraction     5   
1000		 .
.5% =    5   
1000		 .

Therefore, .5% is 5 out of 1000.

b)  .05% is 5 out of how many?

  Solution.   .05% = .0005 =       5    
10,000		 .  Therefore, .05% is 5 out of 10,000.

Compare Lesson 18, Example 7.

Frequent decimals

In the actual practice of arithmetic, changing a fraction to a decimal is an extremely rare event.  (We change a fraction to a percent directly: Lesson 27, Question 3.)  The following are the only fractions whose decimal equivalents come up with any frequency.  The student should know them.

1
2		   1
4		   3
4		   1
8		   3
8		   5
8		   7
8
1
5		   2
5		   3
5		   4
5
1
3		   2
3
Let us begin with  1
2		 .
1
2		  =   5 
10		  = .5  or  .50.
Next,  1
4		 .  But  1
4		  is half of  1
2		 .

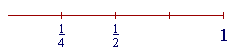
decimals

Therefore, its decimal will be half of .50 --

1
4		   =  .25
  As for  3
4		  , since   3
4		 =  3 ×  1
4		  , then 
3
4		   =  3 × .25  =  .75
Next,  1
8		 .  But  1
8		  is half of  1
4		 .

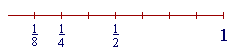
decimals

(Compare Lesson 15.)

Therefore its decimal will be half of .25  or  .250 (Lesson 3) --

1
8		   =  .125

The decimals for the rest of the eighths will be multiples of .125.

Since 3 × 125 = 375,

3
8		   =  3 × .125  =  .375
5
8		  will be 5 ×  1
8		   =  5 × .125.

5 × 125 = 5 × 100  +  5 × 25 = 500 + 125 = 625.

(Lesson 9)  Therefore,

5
8		   = .625
Finally,  7
8		   =  7 × .125.

7 × 125 = 7 × 100  +  7 × 25 = 700 + 175 = 875.

7
8		   =  .875

These decimals come up frequently.  The student should know how to generate them quickly.

  Example 12.   Write as a decimal:   5 
16
  Solution.    5 
16		  will be 5 times   1
16		 .
    Now,   1 
16		  is half of  1
8		  (Lesson 15), which we saw is .125, or, .1250.
    Therefore,   1 
16		  = .0625.
5 × 625  =  5 × 600  +  5 × 25
 
  = 3000 + 125
 
  = 3125.

Therefore,

 5 
16		  = .3125.

Fifths

The student should also know the decimals for the fifths:

 1
 5		  =   2 
10		  = .2

The rest will be the multiples of .2 --

2
5		  =  2 ×  1
5		  = 2 × .2  = .4
 
3
5		  = 3 × .2  = .6
 
4
5		  = 4 × .2  = .8
  Example 13.   Write as a decimal:  8 3
4
  Solution.   8 3
4		  = 8.75

The whole number does not change.  Simply replace the common

  fraction  3
4		  with the decimal .75.

  Example 14.   Write as a decimal:   7
2

Solution.   First change an improper fraction to a mixed number:

7
2		  = 3 1
2		  = 3.5

"2 goes into 7 three (3) times (6) with 1 left over."

Then repalce  1
2		  with .5.

Example 15.    How many times is .25 contained in 3?

  Answer.   .25 =   1
4		 .  And  1
4		  is contained in 1 four times.  (Lesson 21.)
  Therefore,  1
4		 , or .25, will be contained in 3 three times as many times.  It will

be contained 3 × 4 = 12 times.

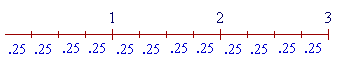
decimals

Example 16.   How many times is .125 contained in 5?

  Answer.   .125 =   1
8		 .  And  1
8		  is contained in 1 eight times.  Therefore,  1
8		  , 

or .125, will be contained in 5 five times as many times.  It will be contained 5 × 8 = 40 times.

As for  1
3		  and  2
3		 , neither one can be expressed exactly as a decimal.

However,

1
3		 approximately .333

and

2
3		 approximately .667

See Section 2, Question 3.

Frequent percents

From the decimal equivalent of a fraction, we can easily derive the percent:  Move the decimal point two digits right.  Again, the student should know these.  They come up frequently.

1
2		   =   .50   =   50%
 
1
4		   =   .25   =   25%
 
3
4		   =   .75   =   75%
 
1
8		   =   .125   =   12.5%  (Half of   1
4		 .
    See Lesson 27, Example 7.)
 
3
8		   =   .375   =   37.5%.   See above.
 
5
8		   =   .625   =   62.5%
 
7
8		   =   .875   =   87.5%
 
1
5		   =   .2   =   20%
 
2
5		   =   .4   =   40%
 
3
5		   =   .6   =   60%
 
4
5		   =   .8   =   80%

In addition, the student should know

1
3		   =  33 1
3		 %
 
2
3		   =  66 2
3		 %

(Lesson 16)


At this point, please "turn" the page and do some Problems.

or

Continue on to the next Section.

Introduction | Home | Table of Contents

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com