4

INFINITY (∞)

The definition of "becomes infinite"

Limits of rational functions

Change of variable

INFINITY, along with its symbol ∞, is not a number and it is not a place. When we say in calculus that a function becomes "infinite," we simply mean that there is no limit to its values.

Let f(x), for example, be . Then as the values of x become smaller and smaller, the values of f(x) become larger and larger. No matter what large number we name, it will be possible to name a value of x such that the value of f(x) will be larger than that number we named.

We then say that the values of f(x) become infinite, or tend to infinity. We say that as x approaches 0, the limit of f(x) is infinity.

Now a limit is a number—a boundary. So when we say that the limit is infinity, we mean that there is no number that we can name.

The student should be aware that the word infinite as it is used in calculus, and has been used historically, does not have the same meaning as in the theory of infinite sets. See this from Wikipedia, especially the views of Carl Friedrich Gauss in the section "Reception of the argument."

When the variable is x and takes on only positive values, then x becomes positively infinite.  We write

If x takes on only negative values, it becomes negatively infinite, in which case we write

In both cases, we mean:  No matter what large number M we name, we get to a point in a sequence of values of x that their absolute values become greater than M.

When the variable is a function f(x), and it becomes positively or negatively infinite when x approaches the value c, then we write

Although we write the symbol "lim" for limit, those algebraic statements mean:  The limit of f(x) as x approaches c does not exist. Again, a limit is a number. (Definition 2.1.)

Definition 4 is the definition of "becomes infinite;" it is not the definition of a limit.

As for the symbol ∞, we employ it in algebraic statements to signify that the definition of  becomes infinite has been satisfied. That symbol by itself has no meaning.

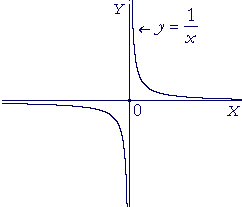
Let us see what happens to the values of y as x approaches 0 from the right:

As the sequence of values of x become very small numbers, then the sequence of values of y, the reciprocals, become very large numbers. The values of y will become and remain greater, for example, than 10^100000000. y becomes infinite.

We write:

If x approaches 0 from the left, then the values of become large negative numbers.  In that case, we write

When a function becomes infinite as x approaches a value c, then the function is discontinuous at x = c, and the straight line  x = c  is a vertical asymptote of the graph. (Topic 18 of Precalculus.)  The graph of y = , then, is discontinuous at x = 0, and the straight line x = c is a vertical asymptote.

Next, let us consider the case when x becomes infinite, that is, when its values become large positive numbers to the extreme right of 0.

In that case, becomes a very small number, namely 0.  We write

We should read that as "the limit as x becomes infinite," not as "x approaches infinity" because again, infinity is neither a number nor a place. On the other hand, we could read that however we please ("the limit as x becomes dizzy"), as long as whatever expression we use refers to the condition of Definition 4.

See First Principles of Euclid's Elements, Commentary on the Definitions. See especially that a definition is nominal; it asserts only how a word or a name will be used; and we must agree to that.

Finally, when x becomes infinite negatively, that is, when it assumes values to the extreme left of 0 (−∞), then again pproaches 0.  We write

In other words, whenever x becomes infinite positively or negatively, the values of  y = approach the horizontal line  y = 0.  That line is called a horizontal asymptote of the graph.

Problem 1.   Evaluate

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!

At   , tan x does not exist.  (Topic 15 and Topic 18 of Trigonometry.)

As x approaches   from the left, tan x becomes larger than any number we might name. (Definition 4.)

Limits of rational functions

A rational function is a quotient of polynomials  (Topic 6 of Precalculus).  It will have this form:

where f and g are polynomials (g 0).

Apart from the constant term, each term of a polynomial will have a factor xⁿ (n ≥ 1).  Therefore let us investigate the following limits.

c could be any positive constant.  The student should complete each right-hand side.

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do it yourself first!

1)		=	0
2a)		=	∞
	n even.
2b)		=	∞
	n odd.
2c)		=	−∞
	n odd.

Compare  y =

1 x

above, where n = 1.

3)		=	∞
4)		=	∞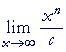

Example.   Prove: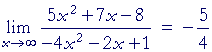

 Solution.   Divide the numerator and denominator by the highest power of x.  In this case, divide them by x²:

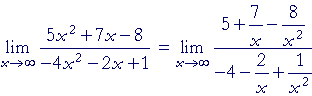
According to 1), above, the limit of each term that contains x is 0.  Therefore by the theorems of Topic 2, we have the required answer.

In similar cases, the first step is:  Divide the numerator and denominator by the power of x that appears in the leading term of either one.

Problem 2.

=

4

The result follows on dividing both numerator and denominator by x.

Problem 3.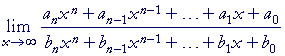

=

In other words:  When the numerator and denominator are of equal degree,
then the limit as x becomes infinite is equal to the quotient of the leading coefficients.

Problem 4.

=

=

=

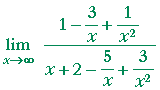0.

In the following, the rational function is the reciprocal of the one above:

=

=

∞

This problem illustrates:

When the degree of the denominator is greater than the degree of the numerator -- that is, when the denominator dominates -- then the limit as x becomes infinite is 0.  But when the numerator dominates -- when the degree of the numerator is greater -- then the limit as x becomes infinite is .

Change of variable

Consider this limit:

Rather than have the variable approach 0, we sometimes prefer that it become infinite.  In that case, we do a change of variable.  We put x = or , it does not matter.  For, x approaching 0 is equivalent to z becoming infinite.  Then

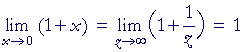
On replacing x with ,  we let z become infinite.  The limit remains 1.

Where will this come up?  In the limit from which we calculate the number e :

(Lesson 15.)

Problem 5.   In the above limit, change the variable to n, and let it become infinite.

Next Lesson:  The derivative

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com