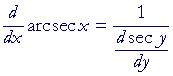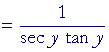 |  |
13
DERIVATIVES OF
INVERSE TRIGONOMETRIC FUNCTIONS
The derivative of y = arcsin x
The derivative of y = arccos x
The derivative of y = arctan x
The derivative of y = arccot x
The derivative of y = arcsec x
The derivative of y = arccsc x
IT IS NOT NECESSARY to memorize the derivatives of this Lesson. Rather, the student should know now to derive them.
In Topic 19 of Trigonometry, we introduced the inverse trigonometric functions. According to the inverse relations:
y = arcsin x implies sin y = x.
And similarly for each of the inverse trigonometric functions.
Problem 1. If y = arcsin x, show:
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Begin:
| y | = | arcsin x | |
| implies | |||
| 1) sin y | = | x. | |
| Therefore, according to the Pythagorean identity a': | |||
| cos y | = |  |
|
| = |  |
||
| according to line 1). | |||
We take the positive sign, because cos y is positive for all values of y in the range of y = arcsin x, which is the 1st and 4th quadrants. (Topic 19 of Trigonometry.) For a similar reason, all the derivatives that follow will have a positive sign.
Problem 2. If y = arcsec x, show:
Begin:
| y | = | arcsec x | |
| implies | |||
| sec y | = | x. | |
| Therefore, according to the Pythagorean identity b: | |||
| tan y | = |  |
|
| = |  |
||
Again, we take the positive sign. tan y is positive for all values of y in the range. (Topic 19 of Trigonometry.)
The derivative of y = arcsin x
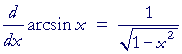
The derivative of the arcsine with respect to its argument
is equal to 1 over the square root
of 1 minus the square of the argument.
Here is the proof:
| y | = | arcsin x | |
| implies | |||
| sin y | = | x. | |
| Therefore, on taking the derivative with respect to x: | |||
 |
= | 1; | |
 |
= |  |
|
|
= |  |
|
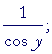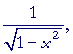according to Problem 1.
Which is what we wanted to prove.
Note: We could have used the theorem of Lesson 8 directly:
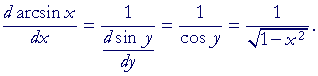
We will use that theorem in the proofs that follow.
Problem 3. Calculate these derivatives. [In parts a) and b), use the chain rule.]
| a) | d dx |
arcsin x² | = |  |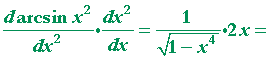
 |
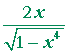| b) | d dx |
 |
= |  |
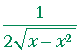| c) | d dx |
x² arcsin x | = |  |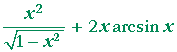
The derivative of y = arccos x
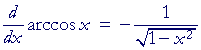
The derivative of arccos x is the negative of the derivative
of arcsin x. That will be true for the inverse of each pair of cofunctions.
The derivative of arccot x will be the negative
of the derivative of arctan x.
The derivative of arccsc x will be the negative
of the derivative of arcsec x.
For, beginning with arccos x:
The angle whose cosine is x is the complement
of the angle whose sine is x.
| arccos x | = | π 2 |
− arcsin x. |
| Since the derivative of | π 2 |
is 0, the result follows. |
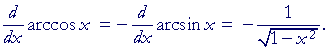
Problem 4. Calculate these derivatives.
| a) | d dx |
arccos | x a |
= |  |
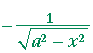| b) | d dx |
x arccos 2x | = |  |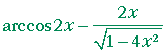
The derivative of y = arctan x
| d dx |
arctan x | = | 1 1 + x² |
First,
y = arctan x implies tan y = x.
Therefore, according to the theorem of Lesson 8:
 |
||
 |
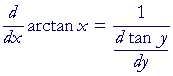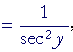Lesson 12, | |
 |
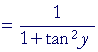, according to the Pythagorean identity b, |
|
 |
||
Which is what we wanted to prove.
Therefore, the derivative of arccot x is its negative:
| d dx |
arccot x | = − | 1 1 + x² |
Problem 5. Calculate these derivatives.
| a) | d dx |
arctan (ax²) | = | 2ax 1 + a2x4 |
| b) | d dx |
arccot | x a |
= | −a a² + x² |
| c) | d dx |
arctan | 2 x |
= | −2 x² + 4 |
| d) | d dx |
arccot 2x | = | −2 4x² + 1 |
The derivative of y = arcsec x
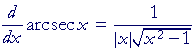
Again,
y = arcsec x implies sec y = x.
Therefore, according to the theorem of Lesson 8:
 |
||
 |
, Lesson 12, | |
 |
according to Problem 2. | |
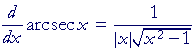
This is what we wanted to prove.
The derivative, therefore, of arccsc x is its negative:
| d dx |
arccsc x | = − |  |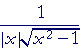
Problem 6. Calculate these derivatives.
| a) | d dx |
arcsec | x a |
= |  |
| b) | d dx |
arcsec | 1 x |
= |  |
| c) | d dx |
arccsc 2x | = |  |
| d) | d dx |
 |
= |  |
Next Lesson: Derivatives of exponential and logarithmic functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2013 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com