30
COMPLEX
OR IMAGINARY
NUMBERS
The square root of a negative number
The real and imaginary components
WHAT ABOUT the square root of a negative number? ![]() ?
?
It cannot be 2, because 2 squared is +4, and it cannot be −2 because −2 squared is also +4. In fact, there is no number, positive or negative, whose square is negative.
However—if we want to say that there is a solution to this equation,
x2 + 4 = 0
then we must say that ![]() is a number. For that equation imples
is a number. For that equation imples
x2 = −4,
x = ±![]() .
.
![]() is not a real number. We call it a complex or imaginary number.
is not a real number. We call it a complex or imaginary number.
Thus symbols such as ![]() ,
, ![]() ,
, ![]() , and so on—the square roots of negative numbers—we will now call complex numbers. Our knowledge of a complex number is, when squared, produces the radicand.
, and so on—the square roots of negative numbers—we will now call complex numbers. Our knowledge of a complex number is, when squared, produces the radicand. ![]() , when squared, produces −3. And so there is nothing to prevent us from making use of those numbers and employing them in calculation. They will obey all the rules we normally associate with a number. We may add them, subtract them, multiply them, and so on.
, when squared, produces −3. And so there is nothing to prevent us from making use of those numbers and employing them in calculation. They will obey all the rules we normally associate with a number. We may add them, subtract them, multiply them, and so on.
Now if a is a positive number, then −a = −1·a. Therefore, according to the theorem:
![]() =
= ![]() =
= ![]()
![]() .
.
The square root of a negative number always leads to the factor ![]() . Hence it will be convenient to put
. Hence it will be convenient to put ![]() equal to i.
equal to i.
![]() = i
= i![]() .
.
We call i the complex unit.
i2 = −1.
That is the fundamental algebraic property of i.
Example 1. 3i · 4i = 12i2 = 12(−1) = −12.
Example 2. −5i · 6i = −30i2 = 30.
We see:
The factor i2 changes the sign of a product.
Problem 1. Evaluate the following.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | i2 = −1 | b) | i · 2i = 2i2 = 2(−1) = −2 | |
| c) | (3i)2 = 32i2 = −9 | d) | −5i · 4i = −20i2 = 20 | |
| Example 3. | = | i |
|
| = | i |
||
| = | i |
||
The square root of −a is equal to i times the square root of a.
Problem 2. Express each of the following in terms of i.
| a) | b) | c) | ||||||
| d) | e) | f) | ||||||
| g) | h) | i) | ||||||
Note: To multiply complex numbers ![]()
![]() , we must first express them in terms of i.
, we must first express them in terms of i.
![]()
![]() = i
= i![]() ·i
·i![]() = −
= −![]() .
.
The rule ![]() does not hold when both a and b are negative.
does not hold when both a and b are negative.
Powers of i
Let us begin with i0, which is 1. (Any number with exponent 0 is 1.) Each power of i can be obtained from the previous power by multiplying it by i. We have:
| i0 | = | 1 |
| i1 | = | i |
| i2 | = | −1 |
| i3 | = | −1· i = −i |
| i4 | = | −i· i = −i2 = −(−1) = 1 |
Since we are back at 1, the cycle of powers will repeat. Any power of i will be either
1, i, −1, or −i
—according to the remainder upon dividing the exponent n by 4.
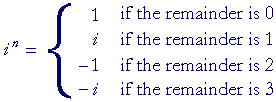
Example 4.
| i9 | = | i, because on dividing 9 by 4, the remainder is 1. | |
| i9 = i1. | |||
| i18 | = | −1, because on dividing 18 by 4, the remainder is 2. | |
| i18 = i2. | |||
| i35 | = | −i, because on dividing 35 by 4, the remainder is 3. | |
| i35 = i3. | |||
| i40 | = | 1, because on dividing 40 by 4, the remainder is 0. | |
| i40 = i0. | |||
Note: Even powers of i will be either 1 or −1, according as the exponent is a multiple of 4, or 2 more than a multiple of 4. While odd powers will be either i or −i.
Problem 3. Evaluate each power of i.
| a) i3 = −i | b) i4 = 1 | c) i6 = i2 = −1 | ||
| d) i9 = i1 = i | e) i12 = i0 = 1 | f) i17 = i1 = i | ||
| g) i27 = i3 = −i | h) i30 = i2 = −1 | i) i100 = i0 = 1 | ||
| Problem 4. |
![]()
![]()
Algebra with complex numbers
Complex numbers follow the same rules as real numbers. For example, to multiply
(2 + 3i)(2 − 3i)
the student should recognize the form (a + b)(a − b) -- which will produce the difference of two squares. Therefore,
| (2 + 3i)(2 − 3i) | = | 4 − 9i2 |
| = | 4 − 9(−1) | |
| = | 4 + 9 | |
| = | 13. | |
Again, the factor i2 changes the sign of the term.
Problem 5. Multiply.
a) (1 + i![]() )(1 − i
)(1 − i![]() ) =
1 − 2i2
=
1 + 2 = 3
) =
1 − 2i2
=
1 + 2 = 3
| b) (3 − i |
= | 9 − 6i |
upon squaring the binomial, |
| = | 9 − 6i |
||
| = | 7 − 6i |
||
| c) (2 + 3i)(4 − 5i) | = | 8 − 10i + 12i − 15i2 |
| = | 8 + 2i + 15 | |
| = | 23 + 2i | |
Problem 6. (x + 1 + 3i)(x + 1 − 3i)
a) What form will that produce? The difference of two squares.
b) Multiply out.
| (x + 1 + 3i)(x + 1 − 3i) | = | (x + 1)2 − 9i2 |
| = | x2 + 2x + 1 + 9 | |
| = | x2 + 2x + 10 | |
| c) | (x − 2 − i |
= | (x − 2)2 − 2i2 |
| = | x2 − 4x + 4 + 2 | ||
| = | x2 − 4x + 6 | ||
The real and imaginary components
Here is what is now called the standard form of a complex number:
a + bi.
It is the real number a plus the complex number ![]() , which is equal to bi.
, which is equal to bi.
For example,
3 + 2i.
a—that is, 3 in the example—is called the real component (or the real part). b (2 in the example) is called the imaginary component (or the imaginary part).
The components are real.
Problem 7. Name the real component a and the imaginary component b.
| a) | 3 − 5i a = 3, b = −5. | b) | 1 + i |
|
| c) | i a = 0, b = 1. | d) | −6 a = −6, b = 0. | |
Complex conjugates
The complex conjugate of a + bi is a − bi. The point about a conjugate pair is that when they are multiplied—
(a + bi)(a − bi)
—the product is a positive real number. That form is the difference of two squares:
(a + bi)(a − bi) = a2 − b2i2 = a2 + b2
The product of a complex conjugate pair
is equal to the sum of the squares of the components.
Problem 8. Calculate the positive real number that results from multiplying each of the following with its complex conjugate.
a) 2 + 3i
(2 + 3i)(2 − 3i) = 22 + 32 = 4 + 9 = 13.
b) 3 − i![]() .
.
(3 − i![]() )(3 + i
)(3 + i![]() ) =
32 + (
) =
32 + (![]() )2= 9 + 2 = 11.
)2= 9 + 2 = 11.
c) u + iv. (u + iv)(u − iv) = u2 + v2.
d) 1 + i. (1 + i)(1 − i) = 12 + 12 = 2.
e) −i. (−i)(i) = −i2 = 1.
Next Lesson: Rectangular coördinates
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
