Simplifying radicals: Section 2
Simplifying the square roots of powers
Simplifying the square roots of powers
Example 4. Since the square of any power produces an even exponent --
(a3)2 = a6
-- then the square root of an even power will be half the exponent.
![]() = a3.
= a3.
As for an odd power, such as a7, it is composed of an even power times a:
a7 = a6a.
Therefore,
![]() =
= ![]() = a3
= a3![]() .
.
(These results hold only for a ≥ 0.)
Problem 5. Simplify each radical. (Assume a ≥ 0.)
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | b) | c) |
| d) | = | = | a |
e) | ||||||||
| f) | = | = | a7 |
g) | = | = | an |
|||||
Note: '2n' in algebra, as in part c), indicates an even number, that is, a multiple of 2. The variable n typically signifies an integer. We signify an odd number, then, as '2n + 1,' as in part g).
Problem 6. Simplify each radical. Remove the even powers. (Assume that the variables do not have negative values.)
| a) | = | 2x |
| b) | = | 2x2y3 |
| c) | = | 3x4yz2 |
Problem 7. True or false? That is, which of these is a rule of algebra? (Assume that a and b do not have negative values.)
| a) |
True. This is the rule, and the only one. The square root of a product is the product of the square roots of each factor. |
| b) |
False. The radicand is not made up of factors, as in part a). |
| c) |
False! The radicand is not made up of factors. |
| d) |
True. |
| e) |
True. The radicand is (a + b)2. |
Problem 8. Express each radical in simplest form.
a) ![]() =
=
![]() = 2
= 2![]() .
.
To simplify a radical, the radicand must be composed of factors!
b) ![]() =
=
![]() = 2a
= 2a![]()
c) ![]() =
=
![]() = 3b
= 3b![]()
Fractional radicand
A radical is in its simplest form when the radicand is not a fraction.
Example 5. The denominator a square number.
When the denominator is a square number, as ![]() , then
, then
| = | 1 2 |
. |
In general,
![]()
For, a · a = a2.
| Example 6.
|
= | The definition of division | ||
| = | 1 2 |
|||
Problem 9. Simplify each radical.
| a) |
1 3 |
b) |
= | 1 3 |
| c) | = | 2 5 |
d) |
= | 5 6 |
Example 7. The denominator not a square number. Simplify ![]() .
.
Solution. When the denominator is not a square number, we have to make it one. In this example, we will multiply it by itself, that is, by 2. But then we must multiply the numerator by 2, also:
| = | = | = | 1 2 |
Example 8. Simplify ![]() . (Assume that the variables do not have negative values.)
. (Assume that the variables do not have negative values.)
Solution. Again, the denominator must be a perfect square. It must be composed of even powers. Therefore, make the denominator into a product of even powers simply simply by multiplying it -- and the numerator -- by bc. Then extract half of the even powers.
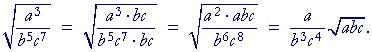
Problem 10. Simplify each radical. (Assume that the variables do not have negative values.)
| a) |
= | 1 3 |
|
b) |
= | 1 5 |
|
| c) |
= | 1 7 |
|
| d) |
= | = | 5 6x |
|
| e) |
= |
2 x2 |
|
f) |
= |
a2 bc2 |
|
| Problem 11. Show | 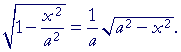 |
A problem that asks you to show, means to write what's on the left, and then transform it algebraically so that it looks like what's on the right.
| Solution. | 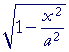 |
= | 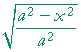 |
= | 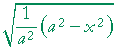 |
= |
We can identify ![]() with the absolute value of x (Lesson 12).
with the absolute value of x (Lesson 12).
![]() .
.
For when x ≥ 0, then
![]() .
.
But if x < 0 -- if, for example, x = −5 -- then
![]()
![]()
because the square root is never negative. (Lesson 26.) Rather, when x < 0, then
![]() .
.
![]() .
.
Therefore in general we must write
![]() .
.
![]() conforms to the definition of the absolute value.
conforms to the definition of the absolute value.
Next Lesson: Multipying and dividing radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com