26
Radicals: Rational and Irrational Numbers
The radical sign and the radicand
Rational and irrational numbers
Which square roots are rational?
An equation x² = a, and the principal square root
The definition of the square root radical
HERE ARE THE FIRST TEN square numbers and their roots:
| Square numbers | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Square roots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
We write, for example,
![]() = 5.
= 5.
"The square root of 25 is 5."
This mark ![]() is called the radical sign (after the Latin radix = root). The number under the radical sign is called the radicand. In the example, 25 is the radicand.
is called the radical sign (after the Latin radix = root). The number under the radical sign is called the radicand. In the example, 25 is the radicand.
Problem 1. Evaluate the following.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | b) | c) | ||||||||
| d) | e) | f) | = | 7 9 |
||||||
Example 1. Evaluate ![]() .
.
Solution. ![]() = 13.
= 13.
For, 13 · 13 is a square number. And the square root of 13 · 13 is 13.
If a is any whole number, then a ·a is a square number, and
![]()
Problem 2. Evaluate the following.
| a) | b) |
| c) |
We have the following theorem:
A square number times a square number is itself a square number.
For example,
36 · 81 = 6 · 6 · 9 · 9 = 6 · 9 · 6 · 9 = 54 · 54
Problem 3. Without multiplying the given square numbers, each product of square numbers is equal to what square number?
a) 25 · 64 = 5 · 8 · 5 · 8 = 40 · 40
b) 16 · 49 = 4 · 7 · 4 · 7 = 28 · 28
c) 4 · 9 · 25 = 2 · 3 · 5 · 2 · 3 · 5 = 30 · 30
Rational and irrational numbers
A rational number is any number of arithmetic: any whole number, fraction, mixed number, or decimal; together with its negative image. A rational number has the same ratio to 1 as two natural numbers.
That is what a rational number is. As for what it looks like, it can take the form of a fraction ![]() , where a and b are integers (b ≠ 0).
, where a and b are integers (b ≠ 0).
Problem 4. Which of the following numbers are rational?
| 1 | −6 | 3½ | 4 5 |
− | 13 5 |
0 | 7.38609 |
All of them.
At this point, the student might wonder, What is a number that is not rational?
An example of such a number is ![]() ("Square root of 2").
("Square root of 2").
![]() is not a number of arithmetic.
is not a number of arithmetic. ![]() is close because
is close because
| 7 5 |
· | 7 5 |
= | 49 25 |
-- which is almost 2.
To see that there is no rational number whose square is 2, suppose there were. Obviously, it is not a whole number. It will be in the form of a fraction in lowest terms. But the square of a fraction in lowest terms is also in lowest terms.
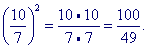
No new factors are introduced and the denominator will never divide into the numerator to give 2—or any whole number.
There is no rational number whose square is 2 or any number that is not a perfect square. We say therefore that ![]() is an irrational number.
is an irrational number.
As a decimal approximation,
![]()
![]() 1.414
1.414
(The wavy equal sign means "is approximately".)
How could we know that? By multiplying 1.414 by itself. If we do, we get 1.999396, which is almost 2. But it should be clear that no decimal multiplied by itself can ever be exactly 2.000000000000000000. If the decimal ends in 1, then its square will end in 1. If the decimal ends it 2, its square will end in 4. And so on. No decimal—no number of arithmetic—multiplied by itself can ever produce 2.
![]() is irrational.
is irrational.
Question. The square roots of which natural numbers are rational?
Answer. Only the square roots of square numbers.
![]() = 1 Rational
= 1 Rational
![]() Irrational
Irrational
![]() Irrational
Irrational
![]() = 2 Rational
= 2 Rational
![]() ,
, ![]() ,
, ![]() ,
, ![]() Irrational
Irrational
![]() = 3 Rational
= 3 Rational
And so on.
Problem 5. Say the name of each number.
| a) | b) | c) |
| d) | 2 5 |
e) |
Problem 6. Which of the following numbers are rational and which are irrational?
a) ![]() Irrational b)
Irrational b) ![]() Rational
Rational
c) ![]() Rational d)
Rational d) ![]() Irrational
Irrational
Only a rational number can we know and name exactly. An irrational number we can know only as a rational approximation.
For the decimal representation of both irrational and rational numbers, see Topic 2 of Precalculus.
An equation x² = a, and the principal square root
Example 2. Solve this equation:
| x² | = | 25. | |
| Solution. | x | = | 5 or −5, because (−5)² = 25, also. |
| In other words, | |||
| x | = | ||
We say however that the positive value, 5, is the principal square root. That is, we say that "the square root of 25" is 5.
![]() = 5.
= 5.
As for −5, it is "the negative of the square root of 25."
−![]() = −5.
= −5.
Thus the symbol ![]() refers to one non-negative number.
refers to one non-negative number.
Example 3. Solve this equation:
| x² | = | 10. | |
| Solution. | x | = | |
Always, if an equation looks like this,
| x² | = | a, | ||
| then the solution will look like this: | ||||
| x | = | |||
| We often use the double sign ± ("plus or minus") and write: | ||||
| x | = | ± |
||
Problem 7. Solve for x.
| a) | x² = 9 implies x = ±3 | b) | x² = 144 implies x = ±12 | |
| c) | x² = 5 implies x = ± |
d) | x² = 3 implies x = ± |
|
| e) | x² = a − b implies x = ± |
|||
Next Lesson: Simplifying radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
