29

RATIONAL EXPONENTS

Fractional exponent

Exponential form vs. radical form

Negative exponent

Evaluations

The rules of exponents

BY THE CUBE ROOT of a, we mean that number whose third power is a.

Thus the cube root of 8 is 2, because 2³ = 8. The cube root of −8 is −2 because (−2)³ = −8.

is the symbol for the cube root of a.  3 is called the index of the radical.

In general,

Read   "The nth root of a."

For example,

, "The 4th root of 81," is 3
because 81 is the 4th power of 3.

If the index is omitted as in , it is the square root; the index is understood to be 2.

Example 1.		=	11.
		=	2   because 25 = 32.
		=	10   because 104 = 10,000.
		=	−2   because (−2)5 = −32.

We see that, if the index is odd, then the radicand may be negative.  But if the index is even, the radicand may not be negative.  There is no such real number as .

Problem 1.   Evaluate each the following -- if it is real.

a)

=

3

b)

=

−3

c)

=

2

d)

=

Not real.

e)

=

−5

f)

=

1

g)

=

Not real.

h)

=

−1

Problem 2.   Prove: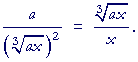

Hint:  Multiply numerator and denominator by

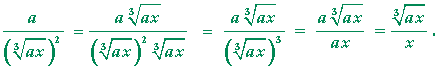
Fractional exponent

We have seen that to square a power, double the exponent.

(a⁴)² = a⁸.

Conversely, then, the square root of a power will be half the exponent. The square root of a⁸ is a⁴; of a¹⁰ is a⁵; of a¹² is a⁶.

This wil[l hold for all powers. The square root of a³ is a. That of a⁵ is a.  And especially, the square root of a¹ is .

In other words, is equal to .

= .

Similarly, since the cube of a power will be the exponent multiplied by 3—the cube of aⁿ is a³ⁿ—the cube root of a power will be the exponent divided by 3. The cube root of a⁶ is a²; of a² is a.  And the cube root of a¹ is a.

a = .

Here is the formal rule:

The denominator of a fractional exponent
is equal to the index of the radical.
The denominator indicates the root.

Example 2.	8  means  The cube root of 8, which is 2.
	81  means  The fourth root of 81, which is 3.
	(−32)  means  The fifth root of −32, which is −2.

8 is the exponential form of the cube root of 8.

is its radical form.

Problem 3.   Evaluate the following.

a)	9  =  3		b)	16  =  4		c)	25  =  5
d)	27  =  3		e)	125  =  5		f)	(−125)  =  −5
g)	81  =  3		h)	(−243)  =  −3		i)	128  =  2
j)	16.25  =  16 = 2

Problem 4.   Express each radical in exponential form

a)

=  x

b)

=

c)

=

(−32)

a is the cube root of a².  The exponent 2 has been divided by 3. However, according to the rules of exponents, it is equal to the square of the cube root:

a = (a)².

That is,

To evaluate a fracitional exponent, it is more efficient to take the root first; for we will then take the power of a smaller number.

For example,

8  =  (8)²  =  2² =  4.

8 is the cube root of 8  squared.

Again:

The denominator of a fractional exponent
indicates the root.

In general,

Problem 5.   Evaluate the following.

a)	27  =  (27)2 = 32 = 9		b)	4  =  (4)3 = 23 = 8
c)	32  =  (32)4 = 24 = 16		d)	(−32)  =  (−2)3 = −8
e)	81  =  (81)5 = 35 = 243		f)	(−125)  =  (−5)4 = 625
g)	9  =  35 = 243		h)	(−8)  =  (−2)5 = −32

Problem 6.   Express each radical in exponential form.

a)	=  x		b)	=  x		c)	=  x
d)	=  x		e)	=  x		f)	=  x

Negative exponent

A number with a negative exponent is defined to be the reciprocal of that number with a positive exponent.

a^−v is the reciprocal of a^v.

Therefore,

1

=

1

=

Problem 7.   Express each of the following with a negative exponent.

a)	1	=	1  x	=	x		b)	1	=	x
c)	1	=	1  x	=	x		d)	1	=	x

Problem 8.   Express in radical form.

a)		=			b)		=	1
c)		=			d)		=

Evaluations

In the Lesson on exponents, we saw that −2⁴ is a negative number. It is the negative of 2⁴.  A minus sign signifies the negative of the number that follows. And the number that follows the minus sign here, −2⁴, is 2⁴.

Similarly, then,

−8 is the negative of 8.

−8  = −2²  = −4.

(−8), on the other hand, is a positive number:

(−8)  =  (−2)²  =  4.

Problem 9.   Evaluate the following.

a)

9−2

=

1  92

=

1  81

b)

9

=

3

c)

9

=

1 3

d)

−9

=

−3

e)

−92

=

−81

f)

(−9)2

=

81

g)

−9−2

=

−

1  81

h)

(−9)−2

=

1  81

i)

−27

=

−9

j)

(−27)

=

9

k)

27

=

1 9

l)

(−27)

=

1 9

Problem 10.   Evaluate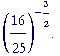

It is the reciprocal of 16/25 -- with a positive exponent.
So it is the square root of 25/16, which is 5/4, then raised to the 3rd power:  125/64.

The rules of exponents

An exponent may now be any rational number.  Rational exponents u, v will obey the usual rules.

auav	=	au + v	Same Base
	=	au − v
(ab)u	=	aubu	Power of a product
(au)v	=	auv	Power of a power
	=		Power of a fraction

Example 3.   Rewrite in exponential form, and apply the rules.

	=	x· x
	=	x
	=	x

See Skill in Arithmetic, Adding and Subtracting Fractions.

Problem 11.   Apply the rules of exponents.

a)	4· 4  =  4  =  4  =  2

b)

8 8

=  8  =  8  =  2

c)

(10)

=  10  =  10−3  =

1    1000

Problem 12.   Express each radical in exponential form, and apply the rules of exponents.

a)	x  =  x· x  =  x  =  x

b)	x2   =  x2· x  =  x  =  x

c)

=

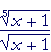(x + 1)  =  (x + 1)

We can now understand that the rules for radicals -- specifically,

-- are rules of exponents.  As such, they apply only to factors.

Problem 13.   Prove:  

 =  (ab) = a· b =  · 

To solve an equation that looks like this:

x	=	b,
take the inverse -- the reciprocal -- power of both sides:
(x)	=	b
x	=	b.

For,  x ·   =  x¹ = x.

Problem 14.   Solve for x.

a)

x

=

8

b)

x

=

−32

x

=

8

=

4

x

=

(−32)

=

−8

c)	(x − 1)	=	64			d)	x7	=	5
x − 1		=	64	x				=
x		=	256 + 1 = 257

e)	x	=	7			f)		=	5
x		=	75	x				=	5  =

Next Lesson:  Complex numbers

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com