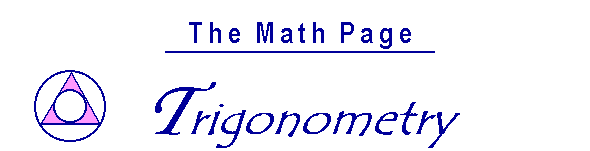
Proof of the reciprocal identities
Proof of the tangent and cotangent identities
Proof of the Pythagorean identities
The proof of each of those follows from the definitions of the trigonometric functions, Topic 15.
Proof of the reciprocal relations
By definition:
| sin θ | = | y r |
, | csc θ | = | r y |
. |
Therefore, sin θ is the reciprocal of csc θ:
| sin θ | = | 1 csc θ |
where 1-over any quantity is the symbol for its reciprocal; Lesson 5 of Algebra. Similarly for the remaining functions.
Proof of the tangent and cotangent identities
To prove:
| tan θ = | sin θ cos θ |
and | cot θ = | cos θ sin θ |
. |
Proof. By definition,
| tan θ = | y x |
. |
Therefore, on dividing both numerator and denominator by r,
| tan θ | = | y/r x/r |
= | sin θ cos θ | . |
| cot θ | = | 1 tan θ |
= | cos θ sin θ | . |
Those are the two identities.
Proof of the Pythagorean identities
To prove:
| a) | sin2θ + cos2θ | = | 1 |
| b) | 1 + tan2θ | = | sec2θ |
| c) | 1 + cot2θ | = | csc 2θ |
Proof 1. According to the Pythagorean theorem,
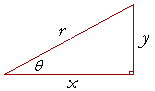
x2 + y2 = r2. . . . . . (1)
Therefore, on dividing both sides by r2,
| x2 r2 |
+ | y2 r2 |
= | r2 r2 |
= 1. |
That is, according to the definitions,
cos2θ + sin2θ = 1. . . . .(2)
Apart from the order of the terms, this is the first Pythagorean identity, a).
To derive b), divide line (1) by x2; to derive c), divide by y2.
Or, we can derive both b) and c) from a) by dividing it first by cos2θ and then by sin2θ. On dividing line 2) by cos2θ, we have
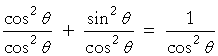
That is,
1 + tan2θ = sec2θ.
And if we divide a) by sin2θ, we have
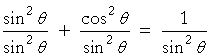
That is,
1 + cot2θ = csc2θ.
The three Pythagorean identities are thus equivalent to one another.
| Proof 2. |  |
| sin2θ + cos2θ | = | y2 r2 |
+ | x2 r2 |
| = | y2 + x2 r2 |
|||
| = | r2 r2 |
|||
| according to the Pythagorean theorem, | ||||
| = | 1. | |||
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com