15
ANALYTIC TRIGONOMETRY
THE UNIT CIRCLE
ANALYTIC TRIGONOMETRY is an extension of right triangle trigonometry. It takes place on the x-y plane. As trigonometry is actually used in calculus and physics, it is not about solving triangles. It becomes the mathematical description of things that rotate or vibrate, such as light, sound, the paths of planets about the sun or satellites about the earth. It is necessary therefore to have angles of any size, and to extend to them the meanings of the trigonometric functions. We do that now.
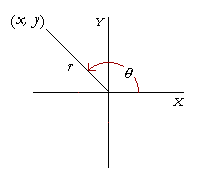
Let a radius of length r sweep out an angle θ in standard position, and let its endpoint have coördinates (x, y). The question is: How shall we now define the six trigonometric functions of θ?
We will take our cue from the first quadrant. In that quadrant,
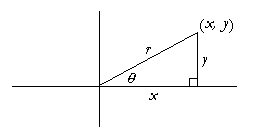
a radius r will terminate at a point (x, y). Those coördinates define a right triangle. The right-triangle definitions of the six trigonometric functions follow.
| sin θ | = | y r |
csc θ | = | r y |
|
| cos θ | = | x r |
sec θ | = | r x |
|
| tan θ | = | y x |
cot θ | = | x y |
|
According to the Pythagorean theorem,
In this way we extend the meaning of the trigonometric functions to angles that terminate in any quadrant. It is in terms of the coördinates (x, y) of the endpoint of a distance r from the origin.
But before we give an example, consider this question:

Will a function of θ depend on the length of r?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Answer the question yourself first!
No, it will not. The functions are defined as the ratios of the sides, not their lengths.
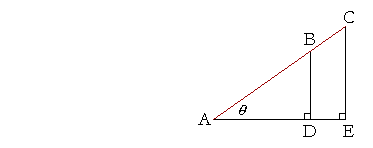
Say that AB, AC are two different radii. But triangles ABD, ACE are similar. Proportionally,
DB : BA = EC : CA
sin θ -- opposite over hypotenuse -- does not depend on the length of the radius. And similarly for the remaining functions. Therefore, we may choose any radius we please. Typically, we take r = 1. That is called the unit circle.
The trigonometric functions in fact depend only on the angle θ -- and it is for that reason we say that they are functions of θ.
Example 1. A straight line inserted at the origin terminates at the point (3, 2) as it sweeps out an angle θ in standard position. Evaluate all six functions of θ.
Answer. x = 3, y = 2. Therefore, according to the definitions:
![]()
| sin θ | = | y r |
= | 2 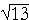 |
csc θ | = | r y |
= | 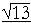 2 |
|
| cos θ | = | x r |
= | 3 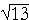 |
sec θ | = | r x |
= | 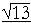 3 |
|
| tan θ | = | y x |
= | 2 3 |
cot θ | = | x y |
= | 3 2 |
|
Problem 1. A straight line from the origin sweeps out an angle θ, and it terminates at the point (3, −4). Evaluate the six functions of θ.
x = 3, y = −4. Therefore,
| sin θ | = − | 4 5 |
csc θ | = − | 5 4 |
|
| cos θ | = | 3 5 |
sec θ | = | 5 3 |
|
| tan θ | = − | 4 3 |
cot θ | = − | 3 4 |
|
Problem 2. The signs in each quadrant.
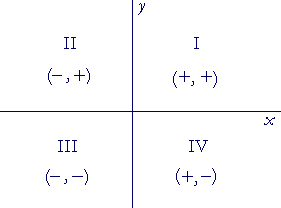
a) The algebraic sign of sin θ will always be the sign of which
a) coördinate? y, because sin θ = y/r, and r is always positive.
a) Therefore, in which quadrants will sin θ -- y -- be positive? I and II.
a) In which quadrants will sin θ be negative? III and IV.
b) The algebraic sign of cos θ will always be the sign of which
b) coördinate? x, because cos θ = x/r, and again, r is always
positive.
a) Therefore, in which quadrants will cos θ -- x -- be positive? I and IV.
a) In which quadrants will cos θ be negative? II and III.
c) In which quadrants will the algebraic sign of tan θ (y/x) be positive?
I and III. x and y will have the same signs.
d) In which quadrants will the algebraic sign of tan θ be negative?
II and IV. x and y will have opposite signs.
e) csc θ will have the same sign as which other function?
sin θ, because they are reciprocals.
f) sec θ will have the same sign as which other function?
cos θ
g) cot θ will have the same sign as which other function?
tan θ
Quadrantal angles
A quadrantal angle is an angle that terminates on the x- or y-axis.
Problem 3.
a) What are the quadrantal angles in degrees?
0°, 90°, 180°, 270°; and angles coterminal with them.
b) What are the quadrantal angles in radians?
| 0, | π 2 |
, π, | 3π 2 |
; and angles coterminal with them. |
c) When an angle terminates on the x-axis, what is the value of the
c) y-coördinate? 0. On the x-axis, y = 0.
d) When an angle terminates on the y-axis, what is the value of the
c) x-coördinate? 0. On the y-axis, x = 0.
Now, it is a fact of arithmetic that there is no number with denominator 0.
| n 0 |
has no meaning. |
Therefore, wherever a trigonometric function has a denominator -- x or y -- equal to 0, at that quadrantal angle the function will have no value.
For example,
| tan θ | = | y x |
Wherever x = 0, tan θ will have no value. Where does x = 0? When the angle terminates on the y-axis.
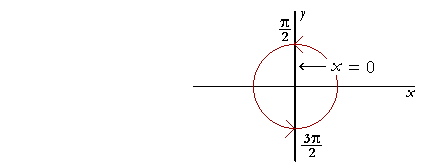
tan θ has no value at θ = ![]() and at
and at ![]() , or at −
, or at −![]() , which is coterminal.
, which is coterminal.
Those values of θ will be singularities of tan θ. (Topic 18 of Precalculus.)
In calculus, the student will encounter the expression, "The limit of ![]() as x approaches 0 = ∞."
as x approaches 0 = ∞."
As explained in Topic 4 of calculus, the word infinity along with its symbol ∞, is not a number and it is not a place. When we say that a function becomes infinite, we simply mean that there is no limit to its values. The function will have values greater than any number that we name.
Note that we say, "As x approaches 0." That is, x may have values as close to 0 as we please. But x may not equal 0.
Problem 4. For which quadrantal angles do the following functions have no value?
| a) cot θ | cot θ = | x y |
. Therefore, whenever y = 0 -- that is, on |
the x-axis -- cot θ will have no value. cot θ will have no value at θ = 0 and θ = π.
b) sec θ
| sec θ = | r x |
. Therefore, sec θ will have no value where x = 0, |
| which is on the y-axis. sec θ will have no value at θ = | π 2 |
| and θ = | 3π 2 |
. |
c) sin θ
| sin θ = | y r |
. But r is never 0. There is no angle for which |
sin θ has no value.
The unit circle
The trigonometric functions are functions only of the angle θ. Therefore we may choose any radius we please, and the simplest is a circle of radius 1, the unit circle.
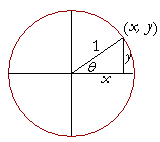
On the unit circle the functions take a particularly simple form. For example,
| sin θ | = | y 1 |
= y. |
| cos θ | = | x 1 |
= x. |
The value of sin θ is the y-coördinate of the endpoint of the unit radius.
The value of cos θ is the x-coördinate.
The following shows the coördinates of the endpoint on the unit circle of every quadrantal angle:
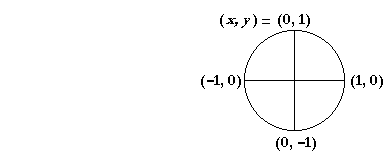
If a function has a value at a quadrantal angle,
it could only be 0, 1, or −1.
Consider sin θ at each quadrantal angle. We just saw that the value of sin θ is the y-coördinate:
sin θ = y.
Therefore at each quadrantal angle, the value of sin θ -- of y -- is either 0, 1, or −1.
| At θ = 0, | sin θ = 0. | |
| At θ = | π 2 |
, sin θ = 1. |
| At θ = π, | sin θ = 0. | |
| At θ = | 3π 2 |
, sin θ = −1. |
To evaluate a function at a quadrantal angle, the student should sketch a unit circle.
Problem 5. Evaluate the following. No tables.
a) cos 0°
cos 0° = 1. cos θ is equal to the x-coördinate.
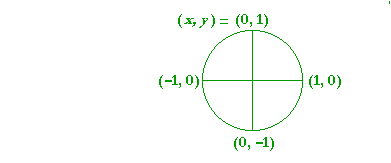
b) cos 90° = 0 c) cos 180° = −1
d) cos 270° = 0
e) tan 0°
tan 0° = 0. tan θ is equal to y/x = 0/1 = 0.
f) tan 90° 1/0 has no value.
g) tan 180° = 0
h) tan 270° has no value.
Problem 6. Evaluate the following -- if it has a value. No tables.
| a) cos | π 2 |
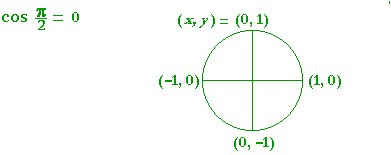
| b) sin | π 2 |
= 1 | c) sin | π | = 0 | d) cos | π | = −1 |
| e) cot 0 | = x/y. No value. | f) cot | π 2 |
= 0 |
| g) tan | π 2 |
No value. | h) sec 0 | = 1/x = 1 |
| i) csc (− | π 2 |
) | = −1 | j) sin 2π | = 0 |
| k) sin 3π | = 0 | l) sin 4π | = 0 |
| m) sin (−π) | = 0 | n) cos 2π | = 1 |
| o) cos 3π | = −1 | p) cos 4π | = 1 |
| q) cos 5π | = −1 |
Problem 7. Explain why we can write the following, where n could be any integer:
cos nπ = (−1)n
(−1)n = ±1, according as n is even or odd. If n is even (or 0), then cos nπ is coterminal with 0 radians, and (−1)n = 1. While if n is odd, then cos nπ is coterminal with π radians, and (−1)n = −1.
See the unit circle.
Radian measure
Since in any circle the same ratio of arc to radius determines a unique central angle, then for theoretical work we often use the unit circle.
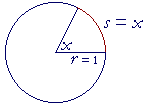
The radian measure is the ratio of arc length s to radius r. Therefore in the unit circle, the the length of the arc s is the radian measure. The length of that arc is a real number x.
s = rθ = 1· x = x.
We can identify radian measure, then, as the length x of an arc of the unit circle. The circumference itself -- 2πr -- has radian measure 2π.
It is here that the term trigonometric "function" has its full meaning. For corresponding to each real number x -- each radian measure, each arc -- there is a unique value of sin x, of cos x, and so on. The definition of a function is satisfied.
Moreover, when we draw the graph of y = sin x, we can imagine the unit circle rolled out in both directions onto the x-axis, and in that way marking the coördinates π, 2π, −π, −2π, and so on, on the x-axis.
Because radian measure can be identified as an arc, the inverse trigonometric functions have their names. "arcsin" is the arc -- the radian measure -- whose sine is a certain number.
| The ratio | sin x x |
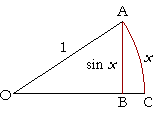
One of the main theorems in calculus concerns the ratio
| sin x x |
for very small values of x.
In the unit circle, side AB opposite angle AOB is sin x.
| sin x | = | AB 1 |
= AB. |
We can see that when the point A on the circumference is very close to C -- that is, when the central angle AOC is extemely small -- then the side AB will be virtually indistinguishable from the arc length AC, which is the radian measure. That is,
| sin x | x | |
| sin x x |
1. | |
Next Topic: Trigonometric Functions of Any Angle
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com