16
TRIGONOMETRIC FUNCTIONS OF ANY ANGLE
HOW SHALL WE EVALUATE tan 120°, for example? We will see that we will be referred back to an acute angle.
The corresponding acute angle
Let θ be an angle that terminates in any quadrant. Then by the corresponding acute angle, we mean the shortest angular distance to the
x-axis.
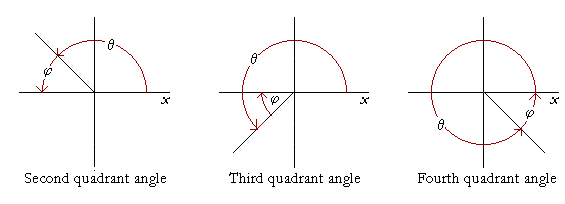
In each quadrant, φ is the corresponding acute angle of θ. φ is the shortest angular distance to the x-axis.
(The corresponding acute angle is often called the reference angle.)
Examples.
If θ = 120° (Second quadrant), then φ = 60°.
If θ = 190° (Third quadrant), then φ = 10°.
If θ = 340° (Fourth quadrant), then φ = 20°.
Problem 1. Name the corresponding acute angle.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
| a) | 150° 30° | b) | 135° 45° | c) | 210° 30° | d) | 315° 45° | |||
| e) | 225° 45° | f) | 240° 60° | g) | 300° 60° | h) | −30° 30° | |||
The theorem
How do we evaluate a function of any angle? The following theorem is the answer.
A function of any angle will equal plus or minus that same function
of the corresponding acute angle.
The sign will depend on the quadrant.
(We will prove that below.)
Example 1. Evaluate tan 120°.
Answer. The corresponding acute angle of 120° is 60°. Therefore, according to the theorem,
tan 120° = ±tan 60° = ±![]()
In the second quadrant, tan θ (y/x) is negative. Therefore,
tan 120° = −![]() .
.
Example 2. Evaluate sec (−45°).
Answer. The corresponding acute angle of −45° (fourth quadrant) is 45°. Therefore,
sec 45° = ±sec 45° = ±![]()
In the fourth quadrant, sec θ (r/x) is positive. Therefore,
sec 45° = ![]()
Problem 2. Draw a figure that illustrates the following.
The sine of an obtuse angle is equal to the sine of its supplement.
The cosine of an obtuse angle is equal to the negative of the cosine
of its supplement.
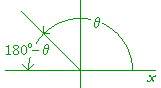
Let θ be an obtuse angle. Then the corresponding acute angle is its supplement, 180° − θ.
sin θ = sin (180° − θ).
cos θ = −cos (180° − θ).
Problem 3. Evaluate each of the following. No tables.
a) sin 150°
The corresponding acute angle is 30°. In the second quadrant, sin θ is positive. Therefore, sin 150° = sin 30° = ½.
b) cos 135°
The corresponding acute angle is 45°. In the second quadrant, cos θ is negative. Therefore, cos 135° = −cos 45° = −½![]() .
.
c) tan 240°
The corresponding acute angle is 60°. In the third quadrant, tan θ is positive. Therefore, tan 240° = tan 60° = ![]() .
.
d) csc (−30)°
The corresponding acute angle is 30°. In the fourth quadrant, csc θ (r/y) is negative. Therefore, csc (−30)° = −csc 30° = −2.
| e) tan | 3π 4 |
| The corresponding acute angle is | π 4 |
See here |
In the 2nd quadrant the tangent is negative. Therefore,
| tan | 3π 4 |
= −1. |
| f) cot | 7π 6 |
| 7π 6 | = 7 · 30° = 210°. |
The corresponding acute angle is 30°. In the 3rd quadrant the costangent is positive. Therefore,
| cot | 7π 6 |
= cot 30° = |
| g) cos | 5π 3 |
| 5π 3 | = 5 · 60° = 300°. |
The corresponding acute angle is 60°. In the 4th quadrant the cosine is positive. Therefore,
| cos | 5π 3 |
= ½. |
Problem 4. What radian angle less than 2π is x?
a) sin x = ½. x = π/6 or 5π/6.
b) tan x = 1. x = π/4 or 5π/4.
c) cos x = −½![]() . x = 3π/4 or 5π/4.
. x = 3π/4 or 5π/4.
We come now to the following theorem:
| cos (−θ) = cos θ. sin (−θ) = −sin θ. |
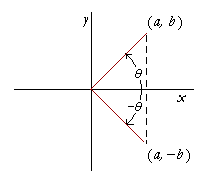
Let (a, b) and (a, −b) be coördinates on a unit circle. Then according to the definitions,
cos θ = a. cos (−θ) = a.
That is,
cos (−θ) = cos θ.
On the other hand,
sin θ = b. sin (−θ) = −b.
That is,
sin (−θ) = −sin θ.
That is what we wanted to prove.
In the language of functions, cos θ is an even function: cos (−θ) = cos θ; while sin θ is an odd function: sin (−θ) = −sin θ.
It follows, then, that the graph of cos x is symmetrical with respect to the y-axis; the graph of sin x, with respect to the origin.
Problem 5. Use the previous theorem to evaluate the following.
a) cos (−30°)
= cos 30° = ½![]()
b) cos (−60°) = cos 60° = ½
c) cos (−45°)
= cos 45° = ½![]()
d) sin (−30°) = −sin 30° = −½.
e) sin (−60°)
= −sin 60° = −![]() /2
/2
f) sin (−45°)
= −sin 45° = −½![]()
Problem 6. Use this figure to prove: tan (−θ) = −tan θ.
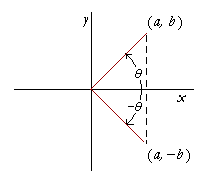
tan θ = b/a. tan (−θ) = −b/a. Therefore, tan (−θ) = −tan θ.
tan θ is an odd function.
Polar coördinates
We can specify the position of a point P by giving its distance r from the origin and the angle θ that r makes with the x-axis. Those are called the polar coördinates of P. (r, θ).
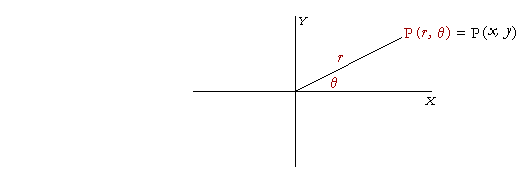
But the polar coördinates are easily related to the rectangular coördinates (x, y). Since
| x r |
= | cos θ |
(Topic 15), then
| x = r cos θ. |
And since
| y r |
= | sin θ, |
| y = r sin θ. |
Example 4. A radius of 8 cm sweeps out an angle of 30° in standard position. What are the rectangular coordinates (x, y) of the endpoint of the radius?
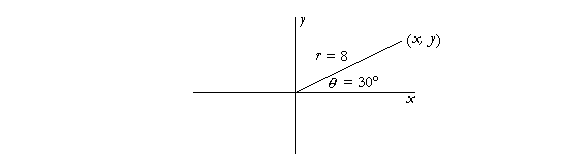
| Answer. | x = r cos θ = 8 cos 30° = 8 · | 2 |
= 4 |
y = r sin θ = 8 sin 30° = 8 · ½ = 4.
Problem 7. Radius AB of a unit circle sweeps out an angle 135°. What are the coordinates of B?
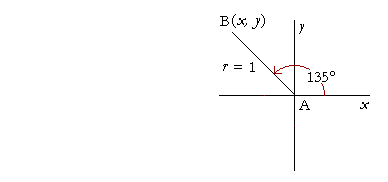
The corresponding acute angle of 135° is 45°. In the second quadrant, the cosine is negative and the sine, positive. Therefore, x = r cos θ = 1· cos 135° = −cos 45° = −½![]() .
.
y = r sin θ = 1· sin 135° = sin 45° = ½![]() .
.
Problem 8. Radius AB of length 2 sweeps out an angle of −60°. What are the coordinates of B?
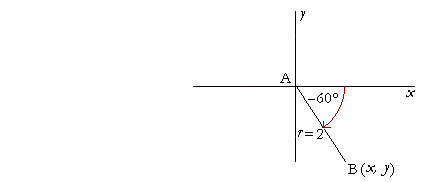
cos (−θ) = cos θ, but sin (−θ) = −sin θ.
Therefore, x = 2· cos (−60°) = 2· cos 60° = 2· ½ = 1.
y = 2· sin (−60°) = 2(−sin 60°) = 2(−½![]() ) = −
) = −![]() .
.
Proof of the theorem
A function of any angle will equal plus or minus that same function
of the corresponding acute angle.
The sign will depend on the quadrant.
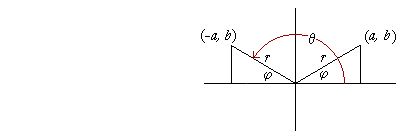
First, if θ is a second quadrant angle, then r will terminate at a point
(−a, b). The corresponding acute angle is φ, which is also shown in its first quadrant position. In the second quadrant,
| sin θ | = | b r |
while in the first quadrant,
| sin φ | = | b r |
Therefore the sine of θ is equal to the sine of the corresponding acute angle.
Similarly,
| cos θ | = − | a r |
= | −cos φ |
| tan θ | = − | b a |
= | −tan φ |
And so on, for the remaining functions, so that in every case, a function of θ is plus or minus that same function of φ.
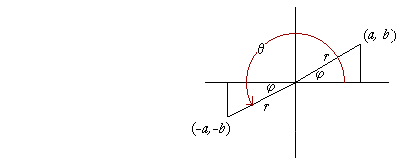
Next, if θ is a third quadrant angle, so that r terminates at (−a, −b), then
| sin θ | = − | b r |
= | −sin φ | |
| cos θ | = − | a r |
= | −cos φ | |
| tan θ | = | −b −a |
= | b a |
= tan φ |
And so on, so that again, each function of θ is plus or minus that same function of φ.
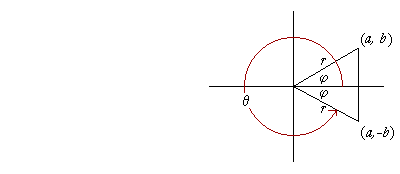
Finally, if θ is a fourth quadrant angle, so that r terminates at (a, −b), then
| sin θ | = − | b r |
= | −sin φ | |
| cos θ | = | a r |
= | cos φ | |
| tan θ | = − | b a |
= | −tan φ | |
Therefore again, each function of θ is plus or minus that same function of the corresponding acute angle φ; which is what we wanted to prove.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com