17
LINE VALUES
THE LINE VALUE of a trigonometric function is a straight line whose length represents the value of the function. For as the central angle changes, the line value becomes a kind of "graph" of the function. It is an excellent way for the student to visualize and remember each function's values, in particular those of the sine, cosine, and tangent.
The line values
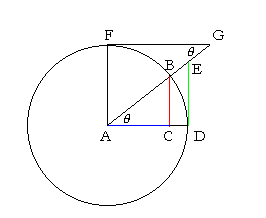
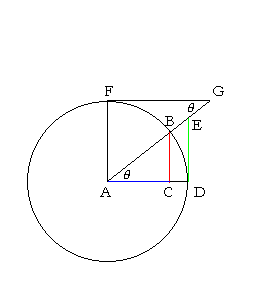
Let A be the center of a unit circle with radii AB, AD.
From B, drop a perpendicular BC onto AD.
Draw radius AF perpendicular to DA; draw DE, FG tangent to the circle; that is, draw them at right angles to the radii; (Theorem 13)
and extend AB to meet those tangents at E, G respectively.
Then, since AG is a straight line that crosses the parallel straight lines FG, AD, the alternate angles FGA, GAD are equal. (Theorem 8)
The right triangles ACB, ADE, GFA are therefore similar.
The line values of the functions of angle θ are now as follows; to avoid scrolling, the figure below is the same:
| sin θ | = | CB BA |
= | CB 1 |
= CB. |
| cos θ | = | AC BA |
= | AC 1 |
= AC. |
| tan θ | = | DE AD |
= | DE 1 |
= DE. |
| csc θ | = | AG FA |
= | AG 1 |
= AG. |
| sec θ | = | AE DA |
= | AE 1 |
= AE. |
| cot θ | = | FG FA |
= | FG 1 |
= FG. |
We now see why the tangent function (DE) is called that: It is in fact a tangent. The secant function (AE) is a secant. It cuts the circle; from the Latin secare, to cut.
A complete period of sin θ
The student should now try to visualize what happens to CB, the line value of sin θ, as AB makes a complete revolution about the unit circle.
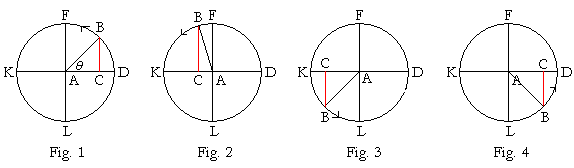
At θ = 0°, the point B coincides with D, so that CB vanishes. sin 0° = 0.
As θ increases in the first quadrant, CB also increases until it reaches its maximum value at 90°. CB coincides there with the unit radius AF, so that CB = AF. sin 90° = 1.
When θ, angle DAB, enters the second quadrant (Fig. 2), CB begins to decrease in value. At 180°, B coincides with K, and CB vanishes again. sin 180° = 0.
In the third quadrant (Fig. 3), CB increases, but the sine in that quadrant is algebraically negative. At 270°, CB coincides with the unit radius AL. sin 270° has its algebraic minimum. sin 270° = −1.
Finally, in the fourth quadrant (Fig. 4), CB decreases until B coincides once again with D. sin 360° = sin 0° = 0.
Upon competing one full circle, sin θ has gone through every possible value. We say that sin θ has completed one period. It is customary to use radian measure, and say that the period of sin θ is 2π.
That means that every 2π radians, 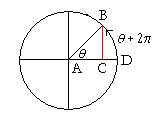 sin θ returns to the same line value CB.
sin θ returns to the same line value CB.
For any angle θ, sin (θ + 2π) = sin θ.
We will go into this again in the following topic.
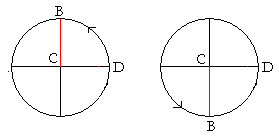
We see moreover that sin θ -- the line value CB -- never has a value greater than 1, which it has at 90°; or less than −1, which it has at 270°.
−1 ≤ sin θ ≤ 1.
A complete period of cos θ
The line value of cos θ is AC. As the terminal side AB revolves, 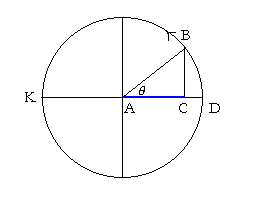 the endpoint C shuttles back and forth along the diameter KD. At 0°, AC coincides with the unit radius AD, so that cos 0° = 1.
the endpoint C shuttles back and forth along the diameter KD. At 0°, AC coincides with the unit radius AD, so that cos 0° = 1.
At θ = 90°, C coincides with A, so that AC vanishes. cos 90° = 0.
At θ = 180°, C reaches K. AC = AK. cos 180° = −1.
At θ = 270°, C is back at A. cos 270° = 0.
Finally, at θ = 360°, AC coincides again with the unit radius AD. cos 360° = 1.
The period of cos θ is also 2π.
cos θ (AC) also has a maximum value of 1, at 0°, and minimum of −1, at 180°.
−1 ≤ cos θ ≤ 1.
A complete period of tan θ
The values of tan θ, like the values of all the trigonometric functions, regularly repeat themselves.
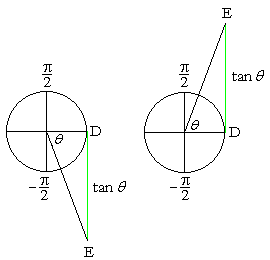
As θ takes on values from 0 to −![]() , or from 0 to
, or from 0 to ![]() , there is no limit to the length of the tangent DE. It is always parallel to the y-axis. In quadrant IV the tangent is negative; in quadrant I, positive. Between −
, there is no limit to the length of the tangent DE. It is always parallel to the y-axis. In quadrant IV the tangent is negative; in quadrant I, positive. Between −![]() and
and ![]() , tan θ assumes all its possible values.
, tan θ assumes all its possible values.
−∞ < tan θ < ∞
The interval from −![]() to
to ![]() constitutes one complete period of tan θ. The period is the distance between those two points: π.
constitutes one complete period of tan θ. The period is the distance between those two points: π.
The graph of a trigonometric function is essentially its line value plotted as the y-coördinate versus radian angle x. See the following Topic: Graphs of the trigonometric functions.
Problem. Which of the following is possible?
a) sin θ = ![]() .
.
Not possible. The values of sin θ are never greater than 1.
See here.
b) cos θ = 2.058
Not possible. The values of cos θ are never greater than 1.
c) tan θ = 2.058
Possible. There is no limit to the values of tan θ.
See here.
d) cot θ = .003
Possible. Since there is no limit to the values of tan θ, there is no limit to the values of its reciprocal.
e) csc θ = ½
Not possible. Since the values of sin θ must be less than or equal to 1, the values of its reciprocal must be greater.
f) sec θ = 5
Possible. Since the values of cos θ must be less than or equal to 1, the values of its reciprocal must be greater.
Projections
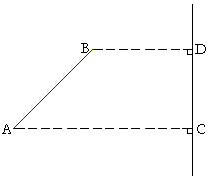
The straight line CD is called the vertical projection of the straight line AB. (The straight lines BD, AC are drawn perpendicular to CD. It is as if a light were shining on AB, and CD is the shadow.)
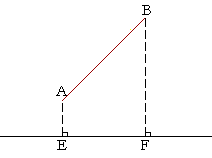
EF is called the horizontal projection of AB.
Now, if AB is a unit radius, the hypotenuse of a right triangle,
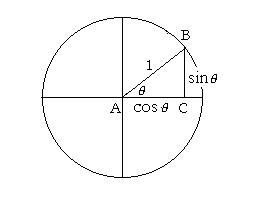
then sin θ is its vertical projection; cos θ, the horizontal projection.
Next Topic: Graphs of the trigonometric functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com