4
RADIAN MEASURE
IN THE RADIAN SYSTEM of angular measurement, the measure of one full circle is 2π.
(In the next Topic, Arc Length, we will see the actual definition of radian measure.)
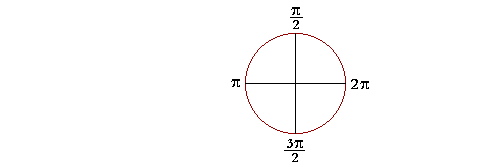
Half a circle, then, is π. And, most important, each right angle is half
| of π: | π 2 |
. |
| Three right angles will be 3· | π 2 |
= | 3π 2 |
. |
| Five right angles will be | 5π 2 |
. And so on. |
Radians into degrees
The following radian measures come up frequently, and the student should know their degree equivalents:
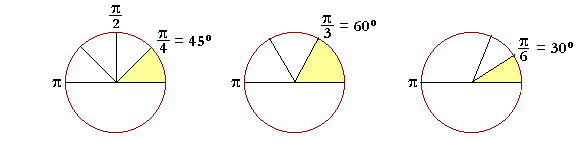
![]() is half of
is half of ![]() , a right angle, and so it is equal to 45°.
, a right angle, and so it is equal to 45°.
Skill in Arithmetic, Lesson 27, Question 4.
| π 3 |
is a third of π, and so is equal to a third of 180°: 60°. |
| π 6 |
is half of | π 3 |
. | π 6 |
= 30°. |
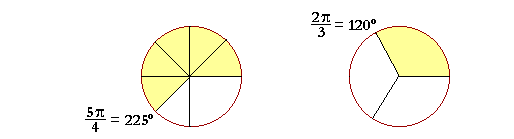
| 5π 4 |
= 5· | π 4 |
= 5· 45° = 225°. |
| 2π 3 |
is a third of 2π. A third of 360° = 120°. |
Problem 1 . Convert each of these radian measures into degrees.
The student should know these.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
| a) π 180° | b) | π 2 |
90° | c) | π 3 |
60° |
| d) | π 6 |
30° | e) | π 4 |
45° |
Problem 2. Convert each of these radian measures into degrees.
| a) | π 8 |
22½°. | π 8 |
is half of | π 4 |
. |
| b) | 2π 5 |
72°. |
| 2π 5 | is a fifth of 2π, which is a fifth of a 360°. |
| c) | 7π 4 |
= 7 · | π 4 | = 7 · 45° = 315° |
| d) | 9π 2 |
= 9 · | π 2 | = 9 · 90° = 810° |
| e) | 4π 3 |
= 4 · | π 3 | = 4 · 60° = 240° |
| f) | 5π 6 |
= 5 · | π 6 | = 5 · 30° = 150° |
| g) | 7π 9 |
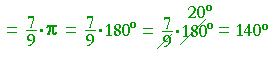 |
Degrees into radians
360° = 2π.
When we write 2π, we mean 2π radians, which is approximately 6.28 radians. However, we normally omit the word radians. As we will see in the next Topic, Arc length, the radian measure can be any real number.
Problem 3. The student should begin by knowing these.
| 0° = | 0 radians. | 360° = | 2π. | 180° = | π. | 90° = | π 2 |
. |
| 45° = | π 4 |
. | 60° = | π 3 |
. | 30° = | π 6 |
. |
Example 1. Convert 120° into radians.
Solution. We can go from what we know to what we do not know. In the most important cases we can recognize the number of degrees as a multiple of 90°, or 45°, or 60°, or 30°; or as a part of 360°.
| Since 60° = | π 3 |
, then |
| 120° = 2· 60° = 2· | π 3 |
= | 2π 3 |
. |
Or, since 120° is a third of 360°, which is 2π, then
| 120° = | 2π 3 |
. |
| Example 2. 225° = 180° + 45° = π + | π 4 |
= | 5π 4 |
. |
Or,
| 225° = 5· 45° = 5· | π 4 |
= | 5π 4 |
. |
Problem 4. Convert each of the following into radians.
| a) 270° = | 3· 90° = | 3π 2 |
b) 210° = | 7· 30° = 7· | π 6 |
= | 7π 6 |
| c) 300° = | 5· 60° = 5· | π 3 |
= | 5π 3 |
| d) 135° = | 3· 45° = 3· | π 4 |
= | 3π 4 |
| e) 720° = | 2· 360° = 2· 2π = 4π |
| f) 450° = | 5· 90° = 5· | π 2 |
= | 5π 2 |
| g) 36° = | A tenth of 360° = | 2π 10 |
= | π 5 |
| h) 72° = | 2· 36° = | 2π 5 |
72° is thus a fifth of a revolution.
| i) 40° = | A ninth of 360° = | 2π 9 |
| j) 80° = | 2· 40° = | 4π 9 |
As a last resort, proportionally,
![]()
so that
![]()
Example 3. Change 140° to radians.
| Solution. | 140 180 |
· π | = | 7 9 |
· π | = | 7π 9 |
, |
upon dividing both the numerator and denominator first by 10 and then by 2. (Lesson 21 and Lesson 1 of Arithmetic.)
Coterminal angles
Angles are coterminal if they have the same terminal side.
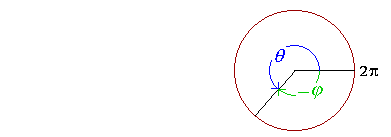
θ is coterminal with −φ. They have the same terminal side.
Notice that
θ + φ = 2π,
so that
θ = 2π − φ . . . . (1)
Example 4. Name in radians the non-negative angle that is coterminal
| with − | 2π 5 |
, and is less than 2π. |
Answer. Let us call that angle θ. Then according to line (1),
| θ = 2π − | 2π 5 |
= | 10π − 2π 5 |
= | 8π 5 |
See Lesson 23 of Algebra, Example 7.
Alternatively, since the numerator is 2π, then ![]() is a fifth of a revolution in the negative direction.
is a fifth of a revolution in the negative direction.
Therefore θ will be four fifths of a revolution in the positive direction.
| θ = | 4 5 |
· 2π = | 8π 5 |
Problem 5. Name in radians the non-negative angle that is coterminal with each of the following, and is less than 2π.
| a) − | 2π 3 |
This is a third of a revolution in the negative direction. Therefore, θ will be two thirds of a revolution in the positive direction.
| θ = | 2 3 |
· 2π = | 4π 3 |
Or:
| θ = 2π − | 2π 3 |
= | 6π − 2π 3 |
= | 4π 3 |
| b) − | π 6 |
θ = 2π − | π 6 |
= | 12π − π 6 |
= | 11π 6 |
| c) − | 3π 4 |
θ = 2π − | 3π 4 |
= | 8π − 3π 4 |
= | 5π 4 |
| d) − | 4π 3 |
θ = 2π − | 4π 3 |
= | 6π − 4π 3 |
= | 2π 3 |
The multiples of π
Starting at 0, let us go around the circle a half-circle at a time. We will then have the following sequence, which are the multiples of π:
0, π, 2π, 3π, 4π, 5π, etc.
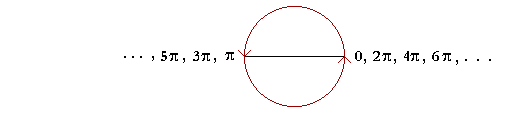
The point to see is that the odd multiples of π --
π, 3π, 5π, 7π, etc.
-- are coterminal with π. While the even multiples of π --
2π, 4π, 6π, etc.
-- are coterminal with 0.
If we go around in the negative direction,
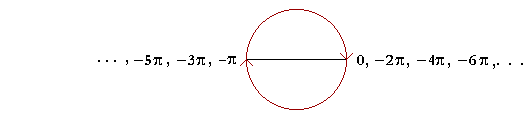
we can make a similar observation.
Problem 6. Name in radians the non-negative angle that is coterminal with each of the following, and is less than 2π.
a) -π π b) -2π 0 c) -3π π
d) -4π 0 e) -5π π
f) 3π π g) 4π 0 h) 5π π
i) 6π 0 j) 7π π
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com