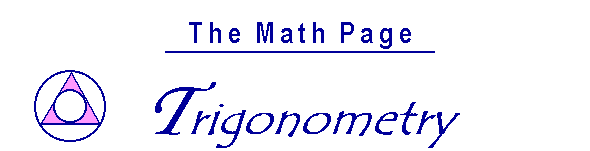
9
THE ISOSCELES RIGHT TRIANGLE
AN ISOSCELES RIGHT TRIANGLE is one of two special triangles. (The other is the 30°-60°-90° triangle.) In each triangle the student should know the ratios of the sides.
(An isosceles triangle has two equal sides. See Definition 8 in Some Theorems of Plane Geometry. The theorems cited below will be found there.)
Theorem. In an isosceles right triangle the sides are in the ratio 1:1:![]() .
.
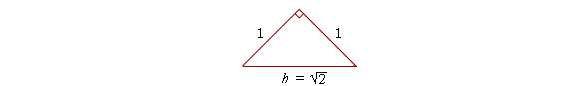
Proof. In an isosceles right triangle, the equal sides make the right angle. They have the ratio of equality, 1 : 1.
To find the ratio number of the hypotenuse h, we have, according to the Pythagorean theorem,
h2 = 12 + 12 = 2.
Therefore,
h = ![]() .
.
(Lesson 26 of Algebra.) Therefore the three sides are in the ratio
1 : 1 : ![]() .
.
Since the triangle is isosceles, the angles at the base are equal. (Theorem 3.) Therefore each of those acute angles is 45°.
(For the definition of measuring angles by "degrees," see Topic 3.)
Example 1. Evaluate sin 45° and tan 45°.
Answer. For any problem involving 45°, the student should sketch the triangle and place the ratio numbers.
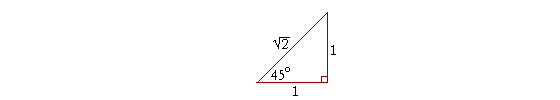
We see:
| sin 45° | = | 1 |
= ½ |
on rationalizing the denominator. (Lesson 26 of Algebra.)
| tan 45° | = | 1 1 |
= 1. |
Problem 1. Evaluate cos 45° and csc 45°.
 |
cos 45° = | 1 |
= ½ |
Thus cos 45° is equal to sin 45°; they are complements.
| csc 45° = | 1 |
= |
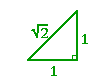
Example 2. Solve the isosceles right triangle whose side is 6.5 cm.
Answer. To solve a triangle means to know all three sides and all three angles. Since this is an isosceles right triangle, the only problem is to find the hypotenuse.
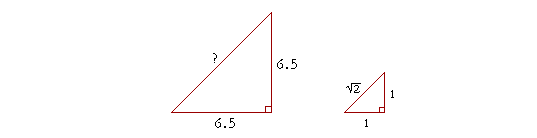
In every isosceles right triangle, the sides are in the ratio 1 : 1 : ![]() , as shown on the right. Those two triangles are similar. The side 1 has been multiplied by 6.5. Therefore every side will be multiplied by 6.5. The hypotenuse will be 6.5
, as shown on the right. Those two triangles are similar. The side 1 has been multiplied by 6.5. Therefore every side will be multiplied by 6.5. The hypotenuse will be 6.5![]() . (The theorem of the same multiple.)
. (The theorem of the same multiple.)
Whenever we know the ratio numbers, then to solve the triangle we use this method of similar figures; not the trigonometric functions.
(In Topic 6, we will solve right triangles the ratios of whose sides we do not know.)
Problem 2. In an isosceles right triangle, the hypotenuse is ![]() inches. How long are the sides?
inches. How long are the sides?
The student should sketch the triangles and place the ratio numbers.
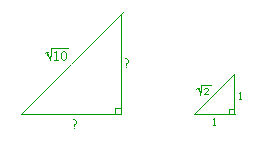
Again, those triangles are similar. The side ![]() has been multiplied by
has been multiplied by ![]() . Therefore, the remaining sides will be multiplied by
. Therefore, the remaining sides will be multiplied by ![]() . Each of the equal sides is 1
. Each of the equal sides is 1![]()
![]() =
= ![]() .
.
Problem 3. Inspect the values of 30°, 60°, and 45° -- that is, look at the two triangles --
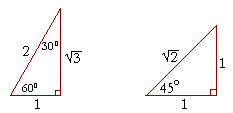
-- and in each equation, decide which of those three angles is the value of x.
| a) | sin x = cos x. x = 45°. | b) | tan x = 1. x = 45°. | ||
| c) | sin x = ½. x = 30° | d) | cos x = ½. x = 60°. | ||
| e) | sin x = ½ |
f) | cos x = ½ |
||
| |
x = 30°. | h) | csc x = 2. x = 30°. |
Problem 4. In radian measure:
| 45° = | π 4 |
. | 60° = | π 3 |
. | 30° = | π 6 |
. |
Problem 5. Evaluate each of the following.
| a) | tan | π 4 |
= 1 | b) | cos | π 3 |
= ½ | c) | sin | π 6 |
= ½ |
| d) | sin | π 4 |
= ½ |
e) | cos | π 4 |
= ½ |
f) | csc | π 6 |
= 2 |
| g) | tan | π 3 |
= |
h) | cot | π 6 |
= |
i) | sec | π 4 |
= |
Next Topic: Solving Right Triangles
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com