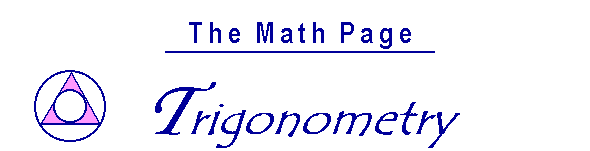
8
THE 30°-60°-90° TRIANGLE
THERE ARE TWO special triangles in trigonometry. One is the 30°-60°-90° triangle. The other is the isosceles right triangle. They are special because with simple geometry we can know the ratios of their sides, and therefore solve any such triangle.
Theorem. In a 30°-60°-90° triangle the sides are in the ratio
1 : 2 : ![]() .
.
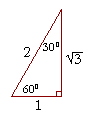
We will prove that below.
Note that the smallest side, 1, is opposite the smallest angle, 30°; while the largest side, 2, is opposite the largest angle, 90°. (Theorem 6). (For, 2 is larger than ![]() . Also, while 1 :
. Also, while 1 : ![]() : 2 correctly corresponds to the sides opposite 30°-60°-90°, many find the sequence 1 : 2 :
: 2 correctly corresponds to the sides opposite 30°-60°-90°, many find the sequence 1 : 2 : ![]() easier to remember.)
easier to remember.)
The cited theorems are from the Appendix, Some theorems of plane geometry.
Here are examples of how we take advantage of knowing those ratios. First, we can evaluate the functions of 60° and 30°.
Example 1. Evaluate cos 60°.
Answer. For any problem involving a 30°-60°-90° triangle, the student should not use a table. The student should sketch the triangle and place the ratio numbers.
Since the cosine is the ratio of the adjacent side to the hypotenuse, we can see that
cos 60° = ½.
Example 2. Evaluate sin 30°.
Answer. According to the property of cofunctions, sin 30° is equal to cos 60°. sin 30° = ½.
On the other hand, you can see that directly in the figure above.
Problem 1. Evaluate sin 60° and tan 60°.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
The sine is the ratio of the opposite side to the hypotenuse.
| sin 60° = | 2 |
= ½ |
The tangent is ratio of the opposite side to the adjacent.
| tan 60° = | 1 |
= |
Problem 2. Evaluate cot 30° and cos 30°.
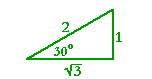
The cotangent is the ratio of the adjacent side to the opposite.
| Therefore, on inspecting the figure above, cot 30° = | 1 |
= ![]() .
.
Or, more simply, cot 30° = tan 60°.
As for the cosine, it is the ratio of the adjacent side to the hypotenuse. Therefore,
| cos 30° = | 2 |
= ½ |
Before we come to the next Example, here is how we relate the sides and angles of a triangle:
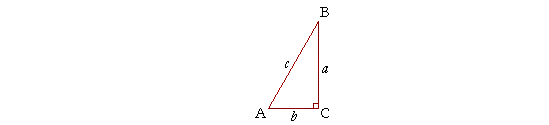
If an angle is labeled capital A, then the side opposite will be labeled small a. Similarly for angle B and side b, angle C and side c.
Example 3. Solve the right triangle ABC if angle A is 60°, and side AB is 10 cm.
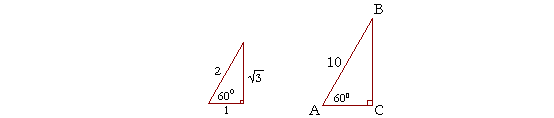
Solution. To solve a triangle means to know all three sides and all three angles. Since this is a right triangle and angle A is 60°, then the remaining angle B is its complement, 30°.
Again, in every 30°-60°-90° triangle, the sides are in the ratio 1 : 2 : ![]() , as shown on the left.
, as shown on the left.
When we know the ratios of the sides, then to solve a triangle we do not require the trigonometric functions or the Pythagorean theorem. We can solve it by the method of similar figures.
Now, the sides that make the equal angles are in the same ratio. Proportionally,
2 : 1 = 10 : AC.
2 is two times 1. Therefore 10 is two times AC. AC is 5 cm.
The side adjacent to 60°, we see, is always half the hypotenuse.
As for BC—proportionally,
2 : ![]() = 10 : BC.
= 10 : BC.
To produce 10, 2 has been multiplied by 5. Therefore, ![]() will also be multiplied by 5. BC is 5
will also be multiplied by 5. BC is 5![]() cm.
cm.
In other words, since one side of the standard triangle has been multiplied by 5, then every side will be multiplied by 5.
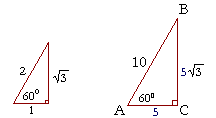
1 : 2 : ![]() = 5 : 10 : 5
= 5 : 10 : 5![]() .
.
Compare Example 11 here.
Again: When we know the ratio numbers, then to solve the triangle the student should use this method of similar figures, not the trigonometric functions.
(In Topic 10, we will solve right triangles whose ratios of sides we do not know.)
Problem 3. In the right triangle DFE, angle D is 30° and side DF is 3 inches. How long are sides d and f ?
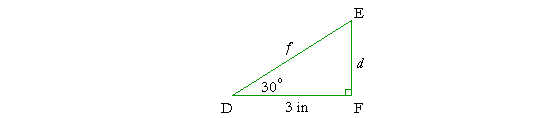

The student should draw a similar triangle in the same orientation. Then see that the side corresponding to ![]() was multiplied by
was multiplied by ![]() .
.
Therefore, each side will be multiplied by ![]() . Side d will be
. Side d will be
1![]()
![]() =
= ![]() . Side f will be 2
. Side f will be 2![]() .
.
Problem 4. In the right triangle PQR, angle P is 30°, and side r is 1 cm. How long are sides p and q ?
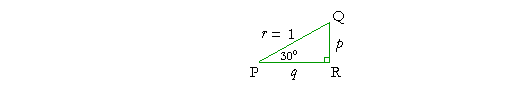

The side corresponding to 2 has been divided by 2. Therefore, each side must be divided by 2. Side p will be ½, and side q will be ½![]() .
.
Problem 5. Solve the right triangle ABC if angle A is 60°, and the hypotenuse is 18.6 cm.
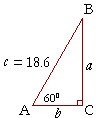
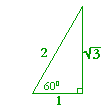
The side adjacent to 60° is always half of the hypotenuse -- therefore, side b is 9.3 cm.
But this is the side that corresponds to 1. And it has been multiplied by 9.3. Therefore, side a will be multiplied by 9.3.
It will be 9.3![]() cm.
cm.
Problem 6. Prove: The area A of an equilateral triangle whose side is s, is
A = ¼![]() s2.
s2.
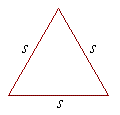
The area A of any triangle is equal to one-half the sine of any angle times the product of the two sides that make the angle. (Topic 2, Problem 6.)
In an equilateral triangle each side is s , and each angle is 60°. Therefore,
A = ½ sin 60°s2.
Since sin 60° = ½![]() ,
,
A = ½· ½![]() s2 = ¼
s2 = ¼![]() s2.
s2.
Problem 7. Prove: The area A of an equilateral triangle inscribed in a circle of radius r, is
| A = | 3 4 |
r2. |
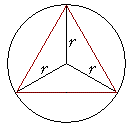
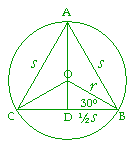
The three radii divide the triangle into three congruent triangles.
Hence each radius bisects each vertex into two 30° angles.
If we extend the radius AO, then AD is the perpendicular bisector of the side CB.
Triangle OBD is therefore a 30-60-90 triangle.
If we call each side of the equilateral triangle s, then in the right triangle OBD,
| ½s r |
= | cos 30° = ½ |
Therefore,
s = ![]() r
r
so that
s2 = 3r2.
Now, the area A of an equilateral triangle is
A = ¼![]() s2.
s2.
Therefore,
| A = ¼ |
= | 3 4 |
That is what we wanted to prove.
Problem 8. Prove: The angle bisectors of an equilateral triangle meet at a point that is two thirds of the distance from the vertex of the triangle to the base.
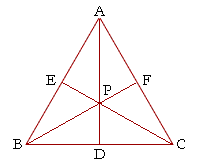
Let ABC be an equilateral triangle, let AD, BF, CE be the angle bisectors of angles A, B, C respectively; then those angle bisectors meet at the point P such that AP is two thirds of AD.
First, triangles BPD, APE are congruent.
For, since the triangle is equilateral and BF, AD are the angle bisectors, then angles PBD, PAE are equal and each
30°;
and the side BD is equal to the side AE, because in an equilateral triangle the angle bisector is the perpendicular bisector of the base.
Angles PDB, AEP then are right angles and equal.
Therefore,
triangles BPD, APE are congruent.

| Now, | BP PD |
= csc 30° = 2. |
Therefore, BP = 2PD.
But AP = BP, because triangles APE, BPD are conguent, and those are the sides opposite the equal angles.
Therefore, AP = 2PD.
Therefore AP is two thirds of the whole AD.
Which is what we wanted to prove.
The proof
Here is the proof that in a 30°-60°-90° triangle the sides are in the ratio 1 : 2 : ![]() . It is based on the fact that a 30°-60°-90° triangle is half of an equilateral triangle.
. It is based on the fact that a 30°-60°-90° triangle is half of an equilateral triangle.
Draw the equilateral triangle ABC. Then each of its equal angles is 60°. (Theorems 3 and 9)
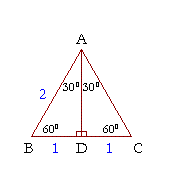
Draw the straight line AD bisecting the angle at A into two 30° angles.
Then AD is the perpendicular bisector of BC (Theorem 2). Triangle ABD therefore is a 30°-60°-90° triangle.
Now, since BD is equal to DC, then BD is half of BC.
This implies that BD is also half of AB, because AB is equal to BC. That is,
BD : AB = 1 : 2
From the Pythagorean theorem, we can find the third side AD:
| AD2 + 12 | = | 22 |
| AD2 | = | 4 − 1 = 3 |
| AD | = |
Therefore in a 30°-60°-90° triangle the sides are in the ratio 1 : 2 : ![]() ; which is what we set out to prove.
; which is what we set out to prove.
Corollary. The square drawn on the height of an equalateral triangle is three fourths of the square drawn on the side.
Next Topic: The Isosceles Right Triangle
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com