12
DERIVATIVES OF
TRIGONOMETRIC FUNCTIONS
THE DERIVATIVE of sin x is cos x. To prove that, we will use the following identity:
sin A − sin B = 2 cos ½(A + B) sin ½(A − B).
(Topic 20 of Trigonometry.)
Problem 1. Use that identity to show:
| sin (x + h) − sin x | = |  |
To see the proof, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| sin (x + h) − sin x | = | 2 cos ½(x + h + x) sin ½(x + h − x) |
| = | 2 cos ½(2x + h) sin ½h | |
| = |  |
|
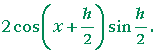Before going on to the derivative of sin x, however, we must prove a lemma; which is a preliminary, subsidiary theorem needed to prove a principle theorem. That lemma requires the following identity:
Problem 2. Show that tan θ divided by sin θ is equal to 
.
| tan θ sin θ |
= | 1 cos θ |
. |
(See Topic 20 of Trigonometry.)
| tan θ sin θ |
= | tan θ · | 1 sin θ |
= | sin θ cos θ |
· | 1 sin θ |
= | 1 cos θ |
The lemma we have to prove is discussed in Topic 14 of Trigonometry. (Take a look at it.) Here it is:
LEMMA. When θ is measured in radians, then
Proof. It is not possible to prove that by applying the usual theorems on limits (Lesson 2). We have to go to geometry, and to the meanings of sin θ and radian measure.
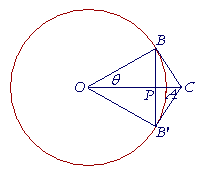
Let O be the center of a unit circle, that is, a circle of radius 1;
and let θ be the first quadrant central angle BOA, measured in radians.
Then, since arc length s = rθ, and r = 1, arc BA is equal to θ. (Topic 14 of Trigonometry.)
Draw angle B'OA equal to angle θ, thus making arc AB' equal to arc BA;
draw the straight line BB', cutting AO at P;
and draw the straight lines BC, B'C tangent to the circle.
Then
BB' < arc BAB' < BC + CB'.
Now, in that unit circle, BP = PB' = sin θ, (Topic 17 of Trigonometry),
so that BB' = 2 sin θ;
| and BC = CB' = tan θ. (For, tan θ = | BC OB |
= | BC 1 |
= BC.) |
The continued inequality above therefore becomes:
2 sin θ < 2θ < 2 tan θ.
On dividing each term by 2 sin θ:
| 1 < | θ sin θ |
< | 1 cos θ |
. |
(Problem 2.) And on taking reciprocals, thus changing the sense:
| 1 > | sin θ θ |
> cos θ. |
(Lesson 11 of Algebra, Theorem 5.)
On changing the signs, the sense changes again :
| −1 < − | sin θ θ |
< | −cos θ, |
(Lesson 11 of Algebra, Theorem 4),
and if we add 1 to each term:
| 0 < | 1 − | sin θ θ |
< | 1 − cos θ. |
Now, as θ becomes very close to 0 (θ 
0), cos θ becomes very close to 1; therefore, 1 − cos θ becomes very close to 0. The expression in the middle, being less than 1 − cos θ, becomes even closer to 0 (and on the left is bounded by 0), therefore the expression in the middle will definitely approach 0. This means:
Which is what we wanted to prove.
The student should keep in mind that for a variable to "approach" 0 or any limit (Definition 2.1), does not mean that the variable ever equals that limit.
The derivative of sin x
| d dx |
sin x | = cos x |
To prove that, we will apply the definition of the derivative (Lesson 5). First, we will calculate the difference quotient.
 |
= |  |
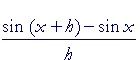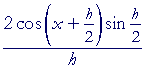, Problem 1, |
| = |  |
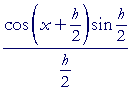, on dividing numerator and denominator by 2, |
|
| = |  |
||
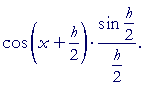We will now take the limit as h 0. But the limit of a product is equal to the product of the limits. (Lesson 2.) And the factor on the right has the form sin θ/θ. Therefore, according to the Lemma, as h 0 its limit is 1. Therefore,
| d dx |
sin x | = cos x. |
We have established the formula.
The derivative of cos x
| d dx |
cos x | = −sin x |
To establish that, we will use the following identity:
| cos x = sin ( | π 2 |
− x). |
A function of any angle is equal to the cofunction of its complement.
(Topic 3 of Trigonometry).
Therefore, on applying the chain rule:
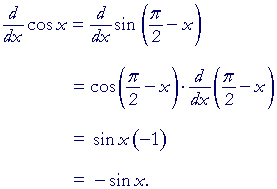
We have established the formula.
The derivative of tan x
| d dx |
tan x = sec2x |
| Now, tan x = | sin x cos x |
. | (Topic 20 of Trigonometry.) |
Therefore according to the quotient rule:
| d dx |
tan x | = | d dx |
sin x cos x |
= | cos x· cos x − sin x(−sin x) cos2x |
||
| = | cos2x + sin2x cos2x |
|||||||
| = | 1 cos2x |
|||||||
| = | sec2x. | |||||||
We have established the formula.
Problem 3. The derivative of cot x. Prove:
| d dx |
cot x = −csc2x |
| d dx |
cot x | = | d dx |
cos x sin x |
||||
| = | sin x(−sin x) − cosx· cos x sin2x |
|||||||
| = | −(sin2x + cos2x) sin2x |
|||||||
| = | − | 1 sin2x |
||||||
| = | −csc2x. | |||||||
The derivative of sec x
| d dx |
sec x | = sec x tan x |
| Since sec x = | 1 cos x |
= | (cos x)−1 | , |
then on using the chain rule and the general power rule:
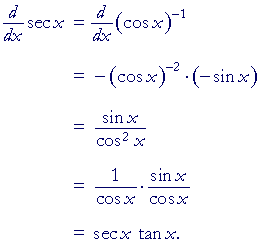
We have established the formula.
Problem 4. The derivative of csc x. Prove:
| d dx |
csc x | = | −csc x cot x |
| d dx |
csc x | = | d dx |
1 sin x |
= |  |
||
| = |  |
|||||||
| = |  |
|||||||
| = |  |
|||||||
| = |  |
|||||||
Example. Calculate the derivative of sin ax2.
Solution. On applying the chain rule,
| d dx |
sin ax2 | = | cos ax2· | d dx |
ax2 | = | cos ax2· | 2ax | = | 2ax cos ax2. |
Problem 5. Calculate these derivatives.
| a) | d dx |
sin 5x | = | 5 cos 5x |
| b) | d dx |
½ sin2x | = | sin x cos x |
| c) | d dx |
2 cos 3x | = | −6 sin 3x |
| d) | d dx |
x cos x | = | cos x − x sin x |
| e) | d dx |
sin 2x cos x | = | 2 cos 2x cos x − sin 2x sin x |
| f) | d dx |
tan (3x)2 | = | 18x sec2 (3x)2 |
| g) | d dx |
2 cot | x 2 |
= | − csc2 | x 2 |
| h) | d dx |
sec 4x | = | 4 sec 4x tan 4x |
| i) | d dx |
a csc bx | = | −ab csc bx cot bx |
| j) |  |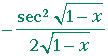
= |  |
Problem 6. ABC is a right angle, and the straight line AD is rotating
so that the angle θ is increasing in the
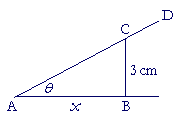positive direction. At what rate -- how many radians per second -- is it increasing if BC is constant at 3 cm, and AB (call it x) is decreasing at the rate of −3 cm/sec, and its length is 6 cm?
 |
|
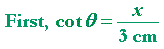| Therefore, | |
| |
| |
| |
| |
 |
|
|
|
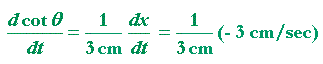
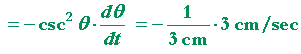
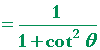
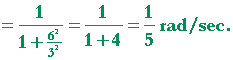
Next Lesson: Derivatives of inverse trigonometric functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com