19
INVERSE TRIGONOMETRIC FUNCTIONS
THE ANGLES in calculus will be in radian measure. Thus if we are given a radian angle, ![]() for example, then we can evaluate a function of it.
for example, then we can evaluate a function of it.
| sin | π 6 |
= | ½. |
(Topic 8.)
Inversely, if we are given that the value of the sine function is ½, then the challenge is to name the radian angle x.
sin x = ½.
"The sine of what angle is equal to ½?"
We write however: Evaluate
arcsin ½.
"The angle whose sine is ½."
The function
y = arcsin x
is called the inverse of the funtion
y = sin x.
arcsin x is the angle whose sine is the number x.
Strictly, arcsin x is the arc whose sine is x. Because in the unit circle, the length of that arc is the radian measure. Topic 15.
Now there are many angles whose sine is ½. It wll be any angle whose corresponding acute angle is ![]() . Therefore we must restrict the range of y = arcsin x -- the values of that angle -- so that it will in fact be a function; so that it will be single-valued.
. Therefore we must restrict the range of y = arcsin x -- the values of that angle -- so that it will in fact be a function; so that it will be single-valued.
How will we do that? We will restrict them to those angles that have the smallest absolute value.
They are called the principal values of y = arcsin x.
Therefore,
arcsin ½ = ![]() .
.
The first quadrant angle ![]() is the angle with the smallest absolute value whose sine is ½.
is the angle with the smallest absolute value whose sine is ½.
Example 1. Evaluate arcsin (−½).
Solution. Angles whose sines are negative fall in the 3rd and 4th quadrants. The angle of smallest absolute value falls in the 4th quadrant between 0 and −![]() .
.
The angle whose sine is −x is simply the negative of the angle whose sine is x.
arcsin (−½) = −arcsin (½) = −![]() .
.
The range, then, of the function y = arcsin x will be angles that fall in the 1st and 4th quadrants, between −![]() and
and ![]() .
.
![]()
Angles whose sines are positive will be 1st quadrant angles. Angles whose sines are negative will fall in the 4th quadrant.
To restrict the range of arcsin x is equivalent to restricting the domain of sin x to those same values. This will be the case with all the restricted ranges that follow.
sin−1x. The inverse sine
Another notation for arcsin x is sin−1x. Read: "The inverse sine of x." −1 here is not an exponent. (See Topic 19 of Precalculus.)
Problem 1. Evaluate the following in radians.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) arcsin 0 = 0. (Topic 15.)
b) arcsin 1 = π/2. (Topic 15.)
c) sin−1 (−1) = −π/2. (Topic 15.)
| |
π/3. (Topic4.) |
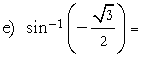 |
−π/3. |
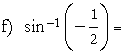 |
−π/6. |
Corresponding to each trigonometric function, there is its inverse function.
arcsin x,
arccos x,
arctan x,
arccsc x,
arcsec x,
arccot x.
In each one, we are given the value x of the trigonometric function. We are to name the radian angle that has that value.
In each case, we must retstrict its range so that the function will be single-valued.
The range of y = arctan x
Like y = arcsin x, y = arctan x has its smallest absolute values in the 1st and 4th quadrants.
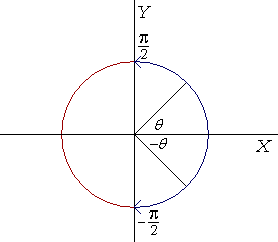
![]()
Note that y -- the angle whose tangent is x -- must be greater than −![]() and less than
and less than ![]() . For at those quadrantal angles, the tangent does not exist.
. For at those quadrantal angles, the tangent does not exist.
Angles whose tangents are positive will be 1st quadrant angles. Angles whose tangents are negative will fall in the 4th quadrant.
That is exactly the same as with arcsin (−x).
The angle whose tangent is −x is simply the negative of the angle whose tangent is x.
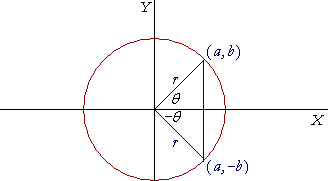
| = | −θ. | |
| = | θ. | |
| Therefore, | ||
| arctan(−x) | = | −arctan x. |
Problem 2. Evaluate the following.
| a) arctan 1 = | π 4 |
b) arctan (−1) = | − | π 4 |
| c) tan−1 |
= | π 3 |
d) tan−1(− |
= | − | π 3 |
| e) arctan 0 = | 0 | f) | = | − | π 6 |
The range of y = arccos x
Example 2. Evaluate arccos ½.
| Solution. | arccos ½ = | π 3 |
. |
| The radian angle whose cosine is ½ is | π 3 |
(60°). |
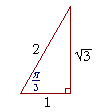
Problem 3. Why is this not true?
arccos (−½) = −![]() .
.
−![]() is a 4th quadrant angle. And in the 4th quadrant, the cosine is positive.
is a 4th quadrant angle. And in the 4th quadrant, the cosine is positive.
An angle whose cosine is negative will fall in the 2nd quadrant, where it will have its smallest absolute value. (Topic 15.)
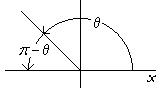
The cosine of a 2nd quadrant angle θ is the negative of the cosine of its corresponding acute angle, which is its supplement.
In other words:
The angle whose cosine is −x
is the supplement of the angle whose cosine is x.
arccos (−x) = π − arccos x.
Example 3. Evaluate arccos (−½).
Solution. We have seen:
arccos ½ = ![]() .
.
Therefore, arccos (−½) is the supplement of ![]() —which is the angle θ that we must add to
—which is the angle θ that we must add to ![]() to equal π.
to equal π.
![]() + θ = π.
+ θ = π.
Now, ![]() is one-third of π. Therefore, its supplement θ will be two-thirds of π:
is one-third of π. Therefore, its supplement θ will be two-thirds of π: ![]() .
.
arccos (−½) = ![]() .
.
The range, then, of y = arccos x will be from 0 to π.
![]()
An angle whose cosine is positive will be a 1st quadrant angle; an angle whose cosine is negative will fall in the 2nd quadrant. It will be the supplement of the 1st quadrant angle.
Problem 4. Evaluate the following.
| a) arccos 1 = | 0 | b) arccos (−1) = | π |
| c) cos−1 | 2 |
= | π 4 |
d) cos−1(− | 2 |
) = | π − | π 4 |
= | 3π 4 |
| e) | 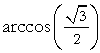 |
= | π 6 |
f) | 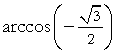 |
= | π − | π 6 |
= | 5π 6 |
| g) arccos 0 = | π 2 |
The inverse relations
If we put
f(x) = sin x
and
g(x) = arcsin x,
then according to the definition of inverse functions:
f(g(x)) = x and g(f(x)) = x.
sin (arcsin x) = x, and arcsin (sin x) = x.
This implies:
arcsin x = θ if and only if x = sin θ.
We have taken the inverse function—the sine—of both sides of the equation on the left. We have extracted the argument x.
For example,
| arcsin ½ = | π 6 |
if and only if ½ = sin | π 6 |
. |
This is in general the case.
Problem 5.
a) arctan t = β if and only if t = tan β.
b) arcsec u = α if and only if u = sec α.
c) arccos 1 = 0 if and only if 1 = cos 0.
| d) arccot 1 = | π 4 |
if and only if | 1 | = cot | π 4 |
. |
This principle enables us to solve many trigonometric equations.
Example 4. Solve for x:
| arcsin (x − 1) = | . |
Solution. By taking the inverse function -- the sine -- of both sides, we can free the argument x − 1. We write immediately:
| x − 1 | = sin | = | 2 |
Therefore,
| x | = 1 + | 2 |
. |
Problem 6. Solve for x:
tan (x + 2) = 1.
| x + 2 | = | arctan 1 = | π 4 |
. |
| x | = | π 4 |
− 2. |
Problem 7. Solve for x:
cos x2 = −1.
x2 = arccos (−1) = π.
x = ±![]() .
.
Problem 8. Solve for x:
| sin−1(x2 − 1) | = | 0. | |
| x2 − 1 | = | arcsin 0 | = 0 |
| x2 | = | 1 | |
| x | = | ±1. | |
The range of y = arcsec x
In calculus, sin−1x, tan−1x, and cos−1x are the most important inverse trigonometric functions. Nevertheless, here are the ranges that make the rest single-valued.
If x is positive, then the value of the inverse function is always a first quadrant angle, or 0. If x is negative, the value of the inverse will fall in the quadrant in which the direct function is negative. Thus if x is negative, arcsec x will fall in the 2nd quadrant, because that is where sec x is negative.
The only inverse function below in which x may be 0, is arccot x. arccot 0 = π/2.
Again, we restrict the values of y to those angles that have the smallest absolute value.
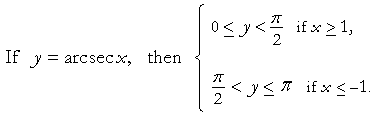
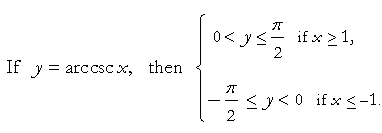
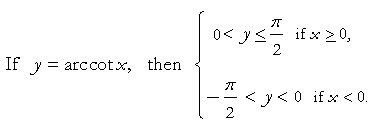
Theorem. If
y = arcsec x,
then the product
sec y tan y is never negative.
For, if y = arcsec x, then the angle y falls either in the first or second quadrants. When angle y falls in the first quadrant, then both sec y and tan y are positive. Therefore their product is positive.
When angle y falls in the second quadrant, sec y and tan y are both negative, so that again their product is positive.
If y = 0, then tan y= 0, hence the product sec y tan y is 0.
Therefore, that product is never negative.
(This theorem is referenced in the proof of the derivative of y = arcsecx.)
Next Topic: Trigonometric identities
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com